標準TTLだけ(!)でCPUをつくろう!(組立てキットです!)
(ホントは74HC、CMOSなんだけど…)
[第554回]
●LOGとLN
Z80BASICの実数演算のサンプルプログラムで、最初にSQR()関数とべき乗について説明をしまして、次に三角関数SIN()、COS()、TAN()の説明をしました。
そうしますと、次はやっぱり対数関数ということになりますでしょう。
なので今回はそのLOG(常用対数)とLN(自然対数)について説明をいたします。
ええ。
Z80BASICには、常用対数も自然対数も、備わっているのです。
まあ、今こうやってあらためて、対数関数の説明をしようとして、よくよく考えてみますと、はて、BASICでLOGなど何に利用できるのだろう?
と疑問を感じてしまいます。
なんでもその昔、計算機などという便利なものがなかった時代には大きな桁数の乗算や除算は大変な労力を必要としたはずで、そのために対数という便利な概念が考え出された、と伝えられております。
とにかく大きな数値同士の乗算、除算で、概算でもよいのだけれどそこそこ正確な答えが欲しい、という場合に、対数を使うと、乗除算が加減算になってしまいますから、そりゃあ便利だったはずです。
ええ。
関数電卓の無かった昔でしたら、確かに。
ですけれど、今はわざわざ対数を使わなくても、大きな数の乗算でも除算でも、あるいは加減乗除が複雑に組み合わさった計算でも、コンピュータという便利なものがあるのですから、あっという間に計算できてしまいます。
おそらく、対数の出番などは無いのでは?
では、なぜに、Z80BASICには、わざわざ苦労してLOG()関数やLN()関数があるのでしょうか?
いや、正直なところ、私自身が疑問に思います。
なぜかといいますと、このZ80BASICを作り上げた当時、そのころはBASICの全盛期でありましたが、他社のBASICを見ますとちゃんと対数関数があるものですから、それならウチでも入れておかにゃあまずいだろう、ということで、それ以上深くは考えないで、LOG()もLN()も使えるようにしてしまったと、多分そのような理由だったのではないかと思います。
まあ、そういう次第で、LOG()やLN()などは、いまどき余り出番の無い関数かも知れませんが、せっかく作ってある機能ですから、ここでご紹介させていただくことに致します。
まずはいつものように単精度実数型のサンプルプログラムです。
>list
10 FOR A=1 TO 10
20 PRINT A,LOG(A),LN(A)
30 NEXT A
>run
1 0 0
2 0.30103 0.693147
3 0.477121 1.09861
4 0.60206 1.38629
5 0.69897 1.60944
6 0.778151 1.79176
7 0.845098 1.94591
8 0.90309 2.07944
9 0.954242 2.19722
10 1 2.30258
たった3行だけの簡単なプログラムです。
昨今はねこもしゃくしもCばかりで、BASICなど見向きもされないようでありますが、この簡便さこそがBASICの一番のウリなのです。
BASICと言いましても、その昔のPC8801とかPC9801の時代のBASICのことで、Visual Basicなどではありません。
昔のBASICは簡便で実に使い易かった、と思います。
さて、上では1〜10の間の常用対数LOG()と自然対数LN()を求めています。
で、この値が正しいかどうか、ということなのですが、LOG()もLN()も三角関数と同様にEXCELで計算して求めることができます。
どうせ、EXCELで求めた結果と付き合わせて評価しよう、ということでしたならば、単精度の計算ではなくて、やっぱり倍精度で計算させた結果とEXCELでの計算結果を比較させてみたいですよねえ。
そこで、今度は倍精度実数演算のLOG()とLN()の計算結果を求めてみました。
>list
10 FOR A#=1# TO 10#
20 PRINT A#,LOG(A#),LN(A#)
30 NEXT A#
>run
1 0 0
2 0.3010299956639812 0.6931471805599454
3 0.4771212547196624 1.09861228866811
4 0.6020599913279624 1.386294361119891
5 0.6989700043360187 1.6094379124341
6 0.7781512503836435 1.791759469228055
7 0.8450980400142567 1.945910149055313
8 0.9030899869919435 2.079441541679836
9 0.9542425094393248 2.197224577336219
10 0.9999999999999999 2.302585092994046
あれ。LOG(10)の計算でわずかな誤差が出てしまいました。
あくまで近似値で計算を行っていることと、10進数ではなくて2進数で計算をしているために、10進数ではきちんと割り切れる数でも、2進数では誤差が残ってしまうことがあります。
実用上は全く問題無い値なのですけれど、このままではちょっと見た目が悪いので、内緒で補正することにいたします。
また、三角関数のときもそうでしたが、倍精度実数演算の計算結果は表示桁数が多いので、縦がきれいに揃わないところが出てきます。そこのところもちょいとPRINT文に手を加えてみました。
>list
10 FOR A#=1 TO 10
20 IF (A#=1)PRINT \5;A#,:PRINT LOG(A#)," ",LN(A#):GOTO 50
30 IF (A#=10)PRINT \5;A#,:PRINT LOG(A#)+0.1D-15," ",LN(A#):GOTO 50
40 PRINT \5;A#,:PRINT LOG(A#),LN(A#)
50 NEXT A#
>run
1 0 0
2 0.3010299956639812 0.6931471805599454
3 0.4771212547196624 1.09861228866811
4 0.6020599913279624 1.386294361119891
5 0.6989700043360187 1.6094379124341
6 0.7781512503836435 1.791759469228055
7 0.8450980400142567 1.945910149055313
8 0.9030899869919435 2.079441541679836
9 0.9542425094393248 2.197224577336219
10 1 2.302585092994046
ご覧の通りの結果が得られました。
LOG(10)だけは、きちんとした値にして表示するために、結果に0.1×10−15を加えています。
倍精度で数値を指数表現するときは、0.1D−15というようにします。
なお0.1E+5のようにEを使うと実数型定数になります。
では、これをEXCELでの計算結果と照合してみましょう。
EXCELでの計算結果です。
a log ln
1 0.0000000000000000 0.0000000000000000
2 0.3010299956639810 0.6931471805599450
3 0.4771212547196620 1.0986122886681100
4 0.6020599913279620 1.3862943611198900
5 0.6989700043360190 1.6094379124341000
6 0.7781512503836440 1.7917594692280500
7 0.8450980400142570 1.9459101490553100
8 0.9030899869919440 2.0794415416798400
9 0.9542425094393250 2.1972245773362200
10 1.0000000000000000 2.3025850929940500
おお。ぴったりではありませんか。
と、言いたいところなのですが、ちょっと気になるところがあります。
LN(6)は、Z80BASICでは末尾が…8055なのに、EXCELでは…8050になっています。
まあ計算末尾だけのことですし、このあたりは誤差の範囲と考えてもいい、と思いますから、無視してもよろしいのですけれど…。
念の為に、Windowsの関数電卓で計算してみました。
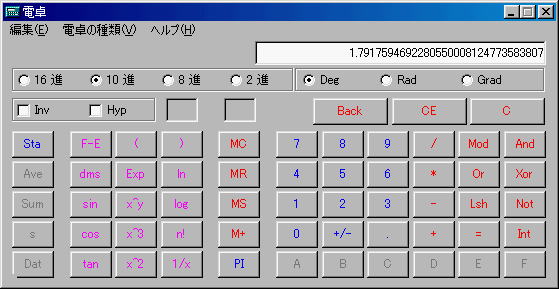
さすがに、有効桁数が違いますねえ。すごいものです。
おお。末尾は、…8055になっています。
お、お、おー。という感じですねえ。
2010.7.16upload
前へ
次へ
ホームページトップへ戻る
