標準TTLだけ(!)でCPUをつくろう!(組立てキットです!)
(ホントは74HC、CMOSなんだけど…)
[第627回]
●USBデバイスの接続手続き(Enumeration)
パソコンのUSBコネクタにUSB機器を接続すると、その装置を特定してそれに合ったデバイスドライバを組み込むために、パソコンのUSBホストコントローラからUSB機器に対して問い合わせの手続きが開始されます。
その問い合わせの手続きは、一連のSETUP(セットアップ)コマンドがホストコントローラから送出され、USB機器がそれに応えて要求された情報を返送する、という形で行われます。
これがEnumeration(エニュミレーション)と呼ばれる初期手続きです。
こいつが実に理解しにくいのですよねえ。
肝心かなめの、そのあたりが理解できるような資料が実に乏しいのです(今でもよくわからない部分も残っているのですけれど)。
いやあ、ドキュメントはどっさりあるのですけれど、本当に知りたいところが、頭が悪いのでしょうかねえ、どうもよくわかりません。
当初はなにをどうすればよいのかもさっぱりわからなくて、本当に苦労しました。
なにしろRS232C通信などとは違って、データの転送速度は桁違いの12MHzですから、オシロスコープなどでは歯が立ちません。
ちなみに一般にパソコンでRS232Cを利用してデータの送受信をする場合には、速くても9600ボーとか19200ボーですから、9.6KHzまたは19.2KHzということになります。
それだけでも大変なのに、それに加えて、さらに信号の中身も複雑です。
RS232Cではパラレルデータの8ビットをそのままシリアルに変換して、それにスタートビットとストップビットを付け加えただけ(パリティなしの場合)ですから、割りと単純です。
ところがUSBの場合には、ただパラレルをシリアルに直しただけではなくて、NRZI変調などというややこしい変調をして、それにCRCビットなどというこれまた単純には解読できそうにないエラー検出ビットまでつけて、そしてそして、さらにそれをトランザクションとかパケットとかという形態で送信、受信するわけですから、こりゃあ、ちょいと信号を覗いて、それで何をやっているのか判断してみようというような簡単なものではありません。
そういえばあれからもうかれこれ1年が経ってしまいそうです。
昨年の秋から暮れのあたり、USBに首をつっこんでしまった当初は、セットアップの仕組み自体もよくわかっていなかったものですから、当然といえば当然のことながら、PIC(当初は18F4550)で、相当に怪しげなUSBのプログラムらしきものを書いて実行させてみても、まともに動作してはくれませんでした。
なんとかして、パソコンのUSBホストコントローラとUSB装置との間の通信を横から掠め取って解読してみることができればUSBプログラムを作成する手がかりをつかむことができるのですけれど。
てなことまで思うようになりました。
とにかく見えなきゃ手の打ちようがない。
なんとかしてラインの状態を見ることはできないものか。
なんでも、そういう装置(USBアナライザ)もあるのだそうですけれど、レンタル料だってン万円とかン十万円とかする高額な測定装置のようですから、そんなものを使うわけにはいきません。
ならば。
自分で作ってしまうより仕方がないでしょう。
ええ。
作ってしまいましたよ。
●自作USBアナライザです
欲しいけれど簡単には手に入らない、というものは、これこの通り、自分で作ってしまうのです。

なんだか実にものものしい雰囲気で、いかにもいかにも、という感じがよく出ていますでしょう。
こちらは裏側の配線の様子です。

回路図です。
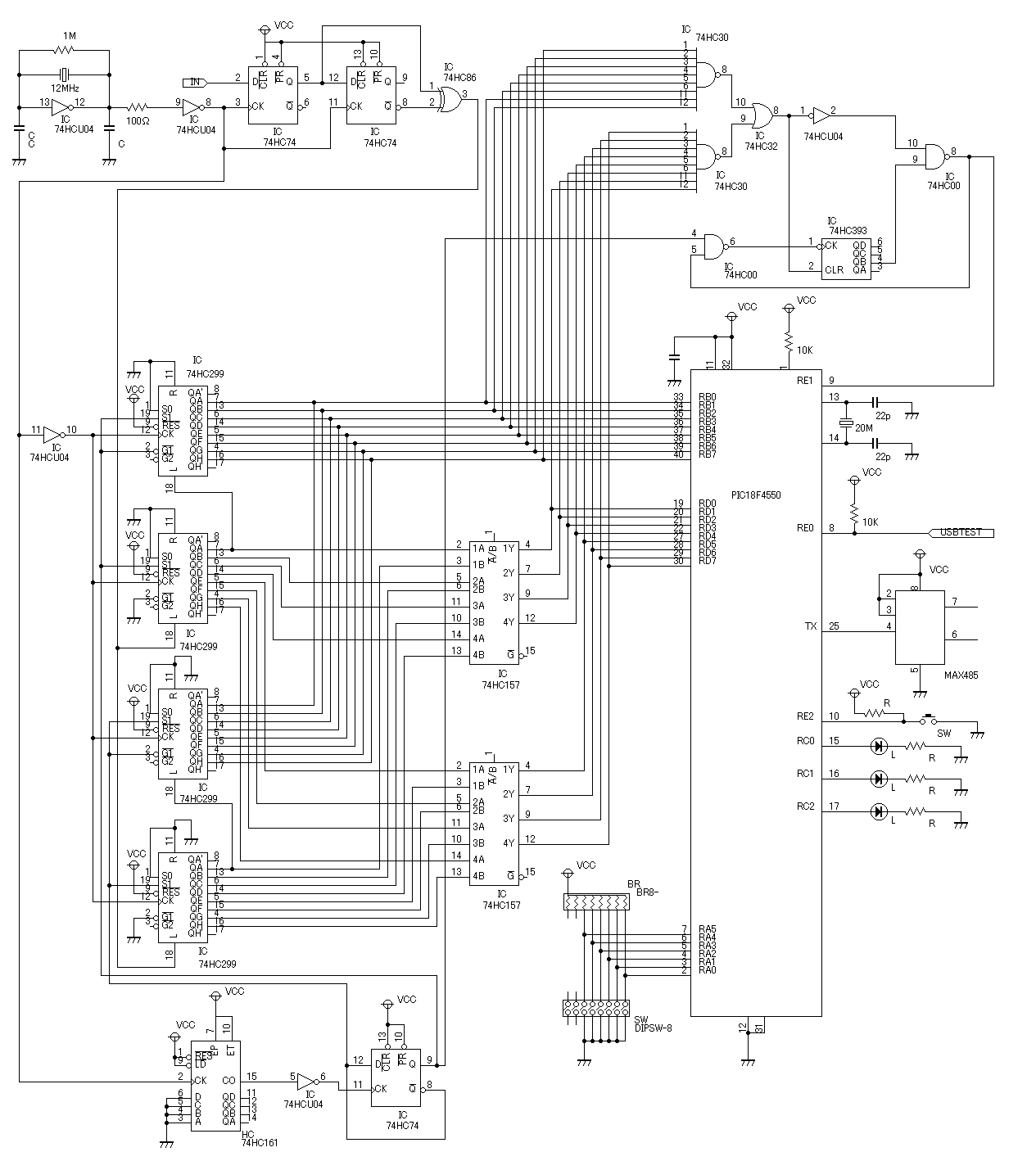
ここでもPIC18F4550を使っていますが、PIC18F4550にはUSB信号は入れません。
USB信号は74HC74のpin2に入ります。
USB信号は上でも説明しましたように非常に高速なので、そもそも信号を記録すること自体が大変なのです。
PIC18F4550はデータロガーとして使っています。
48MHzで動作させていますが、それでもただデータをメモリに蓄えることだけでもタイムオーバーしてしまいます。
74HC回路は復調回路とシリアル→パラレル変換が主な役目ですが、PIC18F4550がタイムオーバーしないようにバッファの役も担っています。
回路の説明を始めますと、また脱線状態になってしまいますから、ここでは省略いたします。
なおNRZI復調は、上の74HC74と74HC86部分です。
CQ出版社「トランジスタ技術」2000年6月号185ページを参考に致しました(というか、まんまです)。
PIC18F4550に蓄えたデータです。
ファイルの日付を確認してみましたら、昨年の12月31日でした。
なにしろ昨年はUSBと格闘(苦闘)しておりましたので、大晦日までがんばっていたのですねえ。
b=0800 11111111 11111111 11111111 11111000 00001101 00101000 10111000 00000011
b=0840 11111111 11111111 11111111 11111111 11111111 11100000 00110100 10110010
b=0880 11100011 11101111 11111111 11111111 11111111 11111111 11111111 11111110
b=08C0 10111110 01100111 11101101 11111111 11111111 11111111 11111111 11111111
b=0900 11111100 00000110 10010111 01011100 00001011 11111111 11111111 11111111
b=0940 11111111 11111111 11110000 00011010 01010011 01110001 11000111 11111111
b=0980 11110000 00011011 01000000 00000000 10001111 11000000 01110000 11000000
b=09C0 01011000 00000000 00100000 00000000 00000000 00000000 10000000 00101110
b=0A00 11001010 01011111 11000000 01010010 11011111 11111111 11111111 11111111
b=0A40 11000000 01101001 01101101 11000000 11011111 11111110 00000011 00101100
b=0A80 00000000 00010001 11111110 00000011 10100100 10010001 00000000 00000000
b=0AC0 10000000 00000000 00000000 00000000 00100001 11010101 11001110 11111000
b=0B00 00001010 01011011 11111111 11111111 11111111 11111111 00000001 10100101
b=0B40 01110111 00000001 11111111 11111111 11111111 11111100 00000110 10010111
b=0B80 11011100 01111011 11111111 11100000 00110000 11100000 00000001 00011111
b=0BC0 10000000 11101001 00000000 00000000 00111111 10000000 10100101 10111111
b=0C00 11111111 11111111 11111111 11111111 11111000 00001101 00101010 10000100
b=0C40 01111111 11111111 11111111 11111111 11111111 11111111 11100000 00110100
b=0C80 10111010 00010010 00011111 11111111 11111111 11111111 11111111 11111111
b=0CC0 10000000 11010010 10011000 01000111 00111111 11111111 11111111 11111111
b=0D00 11111111 11111111 11111111 11111110 00000011 01001011 01100001 00100010
b=0D40 11111111 11111111 11111111 11111000 00001101 00101011 10000100 10011111
b=0D80 11111111 11111111 11111111 11100000 00110100 10111110 00010001 10011111
b=0DC0 11111111 11111111 11111111 00000001 10100101 00001000 10011011 01111111
b=0E00 11111111 11111111 11111100 00000110 10010110 00100010 00010001 11111111
この間は少し省略します。
b=1F00 10010101 11001010 00100111 11111111 11111111 11111111 11110000 00011010
b=1F40 01011111 00101001 01101111 11111111 11111111 11111111 11000000 01101001
b=1F80 01000010 10100000 01011111 11111111 11111111 11111111 00000001 10100101
b=1FC0 10001010 10011110 01111111 11111111 11111111 11111111 11111111 11111000
b=2000 00001101 00101010 01010100 11100111 11111111 11111111 11111111 11111111
b=2040 11111111 11100000 00110100 10111001 01010000 01111111 11111111 11111111
b=2080 11111111 11111111 11111111 10000000 11010010 10010101 01001110 10111111
b=20C0 11111111 11111111 11111111 11111111 11111110 00000011 01001011 01010101
b=2100 00000100 11111111 11111111 10000000 11011010 00000000 00000100 01111110
b=2140 00000011 10000110 00000001 01000000 10000000 00000000 00000000 00000000
b=2180 00000000 00000001 10101110 11010000 11111110 00000010 10010110 11111111
b=21C0 11111111 11111111 11111000 00001101 00101011 01010100 00000111 11111110
b=2200 00000011 00101100 00000000 00010001 11111110 00000011 10100100 00000000
b=2240 00000000 11111000 00001010 01011011 11111111 11111111 11111111 11111111
b=2280 11100000 00110100 10111101 01010011 11111111 11111111 10000000 11010010
b=22C0 10001101 01000111 10111111 11111111 11111111 11111111 11111111 11111111
b=2300 11111111 11111110 00000011 01001011 00110101 00100000 11111111 11111111
b=2340 11111111 11111000 00001101 00101010 11010100 10010111 11111111 11111111
b=2380 10101111 10110111 00111101 01111111 11111111 11111111 11111111 00000001
b=23C0 10100101 00111010 10010011 01111111 11111111 11111111 11111100 00000110
b=2400 10010110 11101010 00110001 11111111 11111111 11111111 11110000 00011010
b=2440 01010111 10101000 11101111 11111111 11111111 11111111 11000000 01101001
b=2480 01111110 01010010 00101111 11111111 11111111 11111111 00000001 10100101
b=24C0 00000110 10010111 11111111 11111111 11111111 11111111 11111111 11111100
b=2500 00000110 10010110 00011010 00100011 11111111 11111111 11111111 11111111
b=2540 11111111 11110000 00011010 01010100 01101000 10100111 11111111 11111111
b=2580 11111111 11111111 11111111 11000000 01101001 01110001 10100101 01011111
b=25C0 11111111 11111111 11111111 11111111 11111111 00000001 10100101 00100110
b=2600 10001011 11111111 11111111 11000000 01101101 00010000 00000101 01011111
b=2640 00000001 11000011 00000001 01100000 00000000 10000000 00011001 10000111
b=2680 11111111 11111111 11111111 11101111 01111111 11111100 11111010 11111111
b=26C0 11111111 11111111 11111000 00001101 00101101 00110100 10100111 11111111
b=2700 10000000 11001011 00100000 00001010 10111111 10000000 11101001 00100100
b=2740 01000000 00000000 00100000 00000000 00000000 00000000 00001000 01110101
b=2780 01110011 10111110 00000010 10010110 11111111 11111111 11111111 11111111
b=27C0 11100000 00110100 10101100 11010010 11001111 11111000 00001100 10110010
b=2800 00000000 10101011 11111000 00001110 00011000 11011001 00000010 10000000
b=2840 00000100 00000000 00000000 00000000 00000111 01111000 11001011 11100000
b=2880 00101001 01101111 11111111 11111111 11111111 11111111 10000000 11010010
b=28C0 11110011 01000100 10111111 11111111 00000001 10010110 01000000 00010101
b=2900 01111111 00000001 11010010 00000000 10000000 11111100 01111000 11111110
b=2940 00000010 10010110 11111111 11111111 11111111 11111110 00000011 01001010
b=2980 00101101 00110011 11111111 11100000 00110000 11101000 00000010 10101111
b=29C0 10000000 11101001 00000000 00000000 00111111 10000000 10100101 10111111
b=2A00 11111111 11111111 11111111 11111111 11111111 11111000 00001101 00101100
b=2A40 10110100 00110111 11111111 11111111 11111111 11100000 00110100 10101010
b=2A80 11010000 10001111 11111111 11100000 00110110 10001000 00000010 10101111
b=2AC0 10000000 11100001 10000000 10110000 00000000 00100000 00000000 00000000
b=2B00 01001000 00000000 00111010 10010000 00111111 10000000 10100101 10111111
b=2B40 11111111 11111111 11111111 11111111 11111111 10000000 11010010 11101011
b=2B80 01001101 10111111 11111100 00000110 01011001 00000000 01010101 11111111
b=2BC0 11110110 11111001 00111111 11111111 11001111 11111001 11111111 11111111
b=2C00 11111111 11101110 11111111 00101011 11110000 00010100 10110111 11111111
b=2C40 11111111 11111111 11111111 11111111 11111110 00000011 01001010 01101101
b=2C80 00001011 11111111 11110000 00011001 01100100 00000001 01010111 11111111
b=2CC0 11011011 10101111 11111111 10011111 11111111 11100000 00101001 01101111
b=2D00 11111111 11111111 11111111 11111111 11111000 00001101 00101101 10110100
b=2D40 11010111 11111111 11000000 01100001 11010000 00000101 01011111 00000001
b=2D80 11010010 00000000 00000000 01111111 11111100 11111010 11111111 11111111
b=2DC0 11111111 10101001 01011110 10111111 11111111 11111111 11111111 11111111
b=2E00 00000001 10100101 11110110 10000111 01111111 11111111 11110000 00011011
b=2E40 01000100 00000001 01010111 11000000 01110000 11000000 01011000 00000000
b=2E80 00010000 00000000 00000000 00111111 01100000 00010010 11100100 10111111
b=2EC0 11100001 11001111 10101111 11111111 11111111 11111111 11111111 11111111
b=2F00 11111111 11111100 00000110 10010100 00111010 01000011 11111111 11100000
b=2F40 00110010 11001000 00000010 10101111 11100000 00111010 01010010 00001000
b=2F80 00010010 10000000 00010000 00010000 00000000 00000000 01111010 00011010
b=2FC0 01101111 10000000 10100101 10111111 11111111 11111111 11111111 11110000
b=3000 00011010 01011000 11101000 11111111 11111111 00000001 10010110 01000000
b=3040 00010101 01111111 00000001 11000011 00000000 10010000 00100000 00000000
b=3080 00000000 01000000 11000000 00000000 01100001 00000010 01111100 00000101
b=30C0 00101101 11111111 11111111 11111111 11111111 11000000 01101001 01010011
b=3100 10100011 01011111 11110000 00011001 01100100 00000001 01010111 11110000
b=3140 00011101 00100000 00000000 00001001 00001000 01001000 10001000 00000000
b=3180 00001000 00000110 10010110 10100111 11000000 01010010 11011111 11111111
b=31C0 11111111 11111111 11111111 00000001 10100101 11001110 10010010 01111111
b=3200 11111100 00000110 01011001 00000000 01010101 11111100 00000111 00001101
b=3240 00010010 11100000 00000011 10000010 10000010 00000111 00000000 00001010
b=3280 10100000 00100001 11110000 00010100 10110111 11111111 11111111 11111111
b=32C0 11111100 00000110 10010100 10111010 00110011 11111111 00000001 10010110
b=3300 01000000 00010101 01111111 11111101 10111111 11111110 01111111 11111110
b=3340 01111110 01111111 11111111 11111111 11111111 11110011 11111001 11111110
b=3380 00000010 10010110 11111111 11111111 11111111 11111111 11110000 00011010
b=33C0 01011010 11101001 00111111 11111110 00000011 00101100 10000000 00101010
b=3400 11111111 11111011 10110110 11111111 11111111 11110101 11111100 00000101
b=3440 00101101 11111111 11111111 11111111 11000000 01101001 01011011 10100100
b=3480 01011111 11111111 11111111 11111111 11111111 11111111 00000001 10100101
b=34C0 11101110 10001110 01111111 11111100 00000110 11011101 11001111 01010101
b=3500 11111111 11011101 11111111 11111111 11111111 11100000 00101001 01101111
b=3540 11111111 11111111 11111111 11111111 11111111 11111000 00001101 00101000
b=3580 11110100 11110111 11111111 11111111 11111111 11100000 00110100 10110011
b=35C0 11010000 00111111 11111111 11111111 11111111 10000000 11010010 10101111
b=3600 01000001 10111111 11111111 11111111 11111110 00000011 01001011 10111101
b=3640 00111000 11111111 11111111 11111111 11111000 00001101 00101001 11110100
b=3680 00010111 11111111 11111111 11111111 11100000 00110100 10110111 11010011
b=36C0 10111111 11111111 11111111 11111111 10000000 11010010 10111111 00100111
b=3700 11111111 11111111 11111111 11111111 11111111 11111110 00000011 01001011
b=3740 11110110 10000000 11111111 11111111 11111111 11111111 11111111 11111000
b=3780 00001101 00101000 00001100 10001011 11111111 11111111 11111111 11111111
b=37C0 11111111 11000000 01101001 01100000 01100011 10011111 11111111 11111111
これじゃあ何もわかりませんよお。
でもないのです。
ビットパターンのままでも根気良く解読していけば、読めないことはありません。
しかし、そりゃあいくらなんでも、愚かのきわみです。
ここは賢くプログラムで解析してみましょう。
暗号の解読みたいなものです。
ええ、ええ。
もちろん解読プログラムも自分で作るのですよ。
なんだって、作れるものは、自分で作ってしまいます。
すると、こうなります。
b=0825 SOF FNO=0E8 [101001010001011100000000]
b=0873 SOF FNO=0E9 [101001011001011100011111]
b=090E SOF FNO=0EB [101001011101011100000010]
b=095C SOF FNO=0EC [101001010011011100011100]
b=098C SETUP [10110100]
b=09B2 DATA0
80 06 00 01 00 00 40 00
b=0A1A ACK
b=0A4A SOF FNO=0ED [101001011011011100000011]
b=0A77 IN ADRS=00 ENDP=00 [1001011000000000000]
b=0A9F DATA1
12 01 00 02 00 00 00 08
b=0B05 ACK
b=0B38 SOF FNO=0EE [101001010111011100000001]
b=0B76 SOF FNO=0EF [101001011111011100011110]
b=0BA3 OUT ADRS=00 ENDP=00 [1000011100000000000]
b=0BC9 DATA1
00 00 FE 80 D2 FE FF FF
b=0C2D SOF FNO=10A [101001010101000010001111]
b=0C7B SOF FNO=10B [101001011101000010010000]
b=0CC9 SOF FNO=10C [101001010011000010001110]
b=0D27 SOF FNO=10D [101001011011000010010001]
b=0D65 SOF FNO=10E [101001010111000010010011]
b=0DA3 SOF FNO=10F [101001011111000010001100]
以下 Frame No.がアップするだけのフレームが続きますから途中を少し省略します(ここは上でも省略したあたりの範囲です)。
b=2005 SOF FNO=152 [101001010100101010011100]
b=2053 SOF FNO=153 [101001011100101010000011]
b=20A1 SOF FNO=154 [101001010010101010011101]
b=20EF SOF FNO=155 [101001011010101010000010]
b=2121 SETUP [10110100]
b=2147 DATA0
00 05 02 00 00 00 00 00
b=21AF ACK
b=21DD SOF FNO=156 [101001010110101010000000]
b=2207 IN ADRS=00 ENDP=00 [1001011000000000000]
b=222F DATA1
00 00 3E A0 B4 FF FF FF
b=22B9 SOF FNO=158 [101001010001101010001111]
b=2317 SOF FNO=159 [101001011001101010010000]
b=2355 SOF FNO=15A [101001010101101010010010]
b=23C0 SOF FNO=15C [101001010011101010010011]
b=23FE SOF FNO=15D [101001011011101010001100]
b=243C SOF FNO=15E [101001010111101010001110]
b=247A SOF FNO=29F [101001011111100101001000]
b=24B8 SOF FNO=160 [101001010000011010010111]
b=2506 SOF FNO=161 [101001011000011010001000]
b=2554 SOF FNO=162 [101001010100011010001010]
b=25A2 SOF FNO=163 [101001011100011010010101]
b=25F0 SOF FNO=164 [101001010010011010001011]
b=2622 SETUP [10110100]
b=2648 DATA0
80 06 00 01 98 E1 FF FF
b=26DD SOF FNO=165 [101001011010011010010100]
b=2709 IN ADRS=02 ENDP=00 [1001011001000000000]
b=2731 DATA1
12 01 00 02 00 00 00 08
b=2797 ACK
b=27CB SOF FNO=166 [101001010110011010010110]
b=27F5 IN ADRS=02 ENDP=00 [1001011001000000000]
b=281D DATA0
D8 04 0A 00 01 00 00 00
b=2883 ACK
b=28B9 SOF FNO=167 [101001011110011010001001]
b=28E8 IN ADRS=02 ENDP=00 [1001011001000000000]
b=2910 DATA1
00 01 3F 1E 7F 40 69 FF
b=2977 SOF FNO=168 [101001010001011010011001]
b=29A3 OUT ADRS=02 ENDP=00 [1000011101000000000]
b=29C9 DATA1
00 00 FE 80 D2 FE FF FF
b=2A35 SOF FNO=169 [101001011001011010000110]
b=2A73 SOF FNO=16A [101001010101011010000100]
b=2AA3 SETUP [10110100]
b=2AC9 DATA0
80 06 00 02 00 00 09 00
b=2B31 ACK
b=2B71 SOF FNO=16B [101001011101011010011011]
b=2B9E IN ADRS=02 ENDP=00 [1001011001000000000]
b=2C2C ACK
b=2C6F SOF FNO=16C [101001010011011010000101]
b=2C9C IN ADRS=02 ENDP=00 [1001011001000000000]
b=2CF3 ACK
b=2D2D SOF FNO=16D [101001011011011010011010]
b=2D5A OUT ADRS=02 ENDP=00 [1000011101000000000]
b=2D80 DATA1
00 00 FE 3F 5F FF FF FF
b=2E08 SOF FNO=16F [101001011111011010000111]
b=2E3C SETUP [10110100]
b=2E62 DATA0
80 06 00 02 00 00 BF 01
b=2F16 SOF FNO=170 [101001010000111010010000]
b=2F43 IN ADRS=02 ENDP=00 [1001011001000000000]
b=2F6B DATA1
09 02 29 00 01 01 00 C0
b=2FD1 ACK
b=3004 SOF FNO=171 [101001011000111010001111]
b=3030 IN ADRS=02 ENDP=00 [1001011001000000000]
b=3058 DATA0
00 09 04 00 00 02 03 00
b=30BE ACK
b=30F2 SOF FNO=172 [101001010100111010001101]
b=311C IN ADRS=02 ENDP=00 [1001011001000000000]
b=3144 DATA1
00 00 09 21 11 01 00 01
b=31AA ACK
b=31E0 SOF FNO=173 [101001011100111010010010]
b=320E IN ADRS=02 ENDP=00 [1001011001000000000]
b=3236 DATA0
22 1D 00 07 05 81 03 40
b=329C ACK
b=32CE SOF FNO=174 [101001010010111010001100]
b=32F8 IN ADRS=02 ENDP=00 [1001011001000000000]
b=3387 ACK
b=33BC SOF FNO=175 [101001011010111010010011]
b=33E7 IN ADRS=02 ENDP=00 [1001011001000000000]
b=343E ACK
b=346A SOF FNO=176 [101001010110111010010001]
b=34B8 SOF FNO=177 [101001011110111010001110]
b=34E6 ? [10110111]
b=3533 ACK
b=3575 SOF FNO=178 [101001010001111010011110]
b=35B3 SOF FNO=179 [101001011001111010000001]
b=35F1 SOF FNO=17A [101001010101111010000011]
b=362F SOF FNO=17B [101001011101111010011100]
b=366D SOF FNO=17C [101001010011111010000010]
b=36AB SOF FNO=17D [101001011011111010011101]
b=36E9 SOF FNO=27E [101001010111111001001111]
b=3737 SOF FNO=2DF [101001011111101101000000]
b=3785 SOF FNO=180 [101001010000000110010001]
b=37D2 SOF FNO=181 [101001011000000110001110]
前述の「トランジスタ技術」誌の同ページの解説記事によりますと、1が連続した場合にはスタッフビットというものが挿入される、と書いてあります。
ここで作ったプログラムは「手抜き」をしていますから、その部分の調整はしていません。
なのでまともに解読はできないかも、と思ったのですけれど、案ずるより産むが易し、で上の解読結果のように、十分役に立ちました。
USBについては、今回はここまでといたします。
また次回に説明をいたします。
●[23]スピーカーの製作(ND80ZⅢ組立説明書の続きです)
TK80の応用プログラムの中にはスピーカーから音を出すものもあります。
といってもいまどきのパソコンのようなオーディオ機能とは比べ物にはなりません。
パソコンに内臓している、警告音用のビープ程度のものです。
それでもプログラムの作り方によっては、十分メロディとして認識できる程度の出力を得ることも可能です。
スピーカーは[10]でプリント基板に取り付けた3.5Φジャックに接続します([第622回]参照)。
そのためには、スピーカーと3.5Φプラグとをビニール被覆線でつなぐ必要があります。
その作業はICのハンダ付けなどよりも難しいところがあります。
以下の図と説明をよく読んでゆっくりていねいに作業してください。
(1)ビニール被覆線の皮むき
まずビニール被覆線の両端の皮むきをします。
①最初にビニール被覆線(平行コード)の両端の色の境目にニッパーかハサミで少し切れ目を入れます。
②そのまま1~2cm切り分けるか、指でつまんで広げます。
③先端5~10mm程度の被覆をむきます。
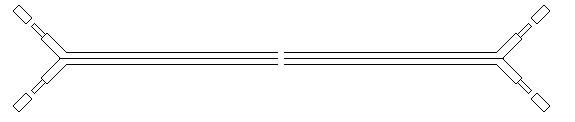
ビニール被覆線の皮むきについては下の図を参考にしてください。
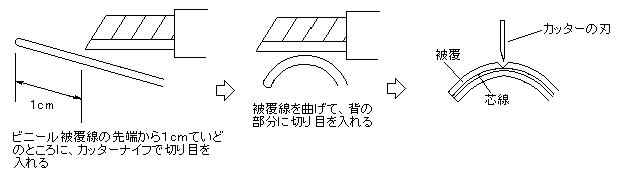
[図の説明]
被覆線を曲げて、背の部分に軽く切り目を入れます。
するとビニールの被覆が「曲げ」のためにひっぱられて切り目に自然に口が開いて、切り目が広がる感じになります。
この状態で少しずつ刃を深く入れながら切っていくと、芯線が見えてくるので、そこで切るのを止めます。
ビニール被覆線を少し回して、まだ切り目を入れていない部分に、同じようにして切り目を入れていきます。
それを繰り返して、被覆線の周り360度の全部に、芯線が見えるまで切り目を入れます。
あとは、被覆線の先端を指でつまんで引き抜くと、被覆の先が抜けるので、芯線を傷つけることなく、きれいに皮むきができます。
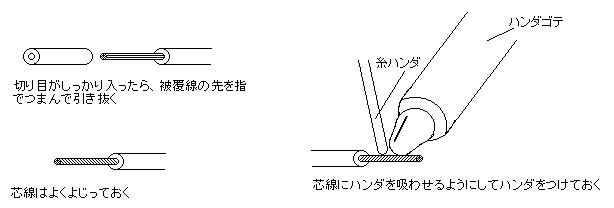
被覆をむいた線は、先にハンダをしっかりとつけておきます(これを「ハンダあげ」といいます)。
被覆線をハンダ付けする場合には、ヒゲが出ていたりして、回路のほかの部分や他方の線とショートすることがありますから、そのようなことがないように注意しながら丁寧にハンダ付けをしてください。
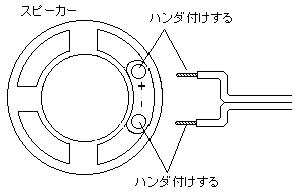
(2)ビニール被覆線の片方の先をスピーカーにハンダ付けする
ビニール被覆線の皮むきをした片方の端をスピーカーにハンダ付けします。
小型のスピーカーなので、+-は余り関係はありませんが、できればこのあと3.5Φプラグを取り付けるときと極性を合わせておくとよいでしょう。
この段階では被覆線のどちらの色を+、-のどちらに接続するかは自由に決めて構いません。
(3)3.5Φプラグを取り付ける
この作業は少し難しいですから、図と説明をよく見て丁寧に作業してください。
①3.5Φプラグのカバーと端子部分は、ねじ込みになっています。
まず、端子からカバーを外します。
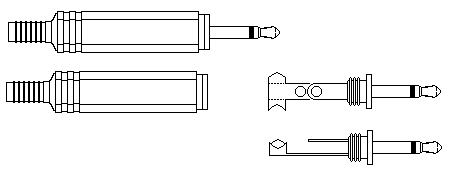
②次にスピーカーに取り付けた被覆線の反対側から下図のように3.5Φプラグのカバーを通します。
これを忘れてしまうと、あとからはカバーを通すことができません。忘れないようにしてください。
また通す向きを間違えないように注意してください。

③被覆線の皮をむいた先端を3.5Φプラグにハンダ付けします。
ちょっと難しいハンダ付けです。
図を良く見て、丁寧に作業してください。
3.5Φプラグの端子の長い側が-で短い側が+です。
先ほどのスピーカーに取り付けたときの+、-と合わせて取り付けた方が良いでしょう。
端子部分の面積が広いため、ちょっとハンダゴテを当てた位ではなかなかハンダがつきません。
端子のハンダ付をするあたりに見当をつけて、先にハンダをあるていどつけておくと、そこに被覆線の先端をあててハンダゴテを当てると、割りと楽にハンダが溶けてくれます。
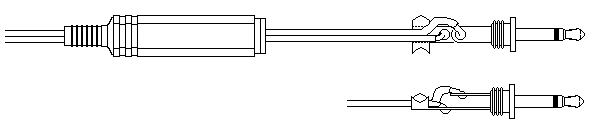
④長いほうの端子のT字に開いている部分を、プライヤーかペンチで曲げて、ビニール被覆線を押さえます。
このとき余り強く押さえすぎて、端子の先端が+側の被覆を破ったりすると、-と+の信号がショートして音が出なくなりますから、そのようなことのないように、注意して作業をしてください。

⑤最後にカバーを元通りに戻せば出来あがりです。
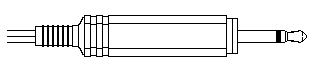
2010.10.4upload
前へ
次へ
ホームページトップへ戻る