16ビットマイコンボードの製作
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
いつか使ってみるつもりで入手してそのまま置いてあった16ビットCPUのことを思い出しました。
AMD社のAM188です。
その名の通り、CPUコアは80188互換の16ビットCPUです。
そのAM188を使った16ビットマイコンボードの製作記事です。
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
[第37回]
●10進実数と2進浮動小数点数
前回の誤差の問題ですが。
SID()関数のテストのときのように0度から90度までを5度きざみにFOR〜NEXT文で回す分には、誤差は発生しません。
最後はきっちり=90になって終ります。
ところがAにラジアン値を入れて、刻み値をPI/36にした場合、PI/36に誤差があるため、それをFOR〜NEXTで加算していくと、最後はきっちりPI/2にならないので、前回の対策のようなことが必要になってきます。
正直な話、これは2進数だからそうなる、ということではありません。
刻み値が端数の場合10進数で計算してもFOR〜NEXTで加算を繰り返せば誤差が蓄積してきます。
ですので前回の例は内部で2進数の浮動小数点演算をやっているから誤差が発生する、ということではなくて、もともとPI/2とかPI/36とかという割り切れない数を扱っているから、と考えるべきです。
そういうことなのですが、前回のところでは、私もちょっと思い違いをしてしまったところがあって、それが2進数の浮動小数点計算だから、と言いたげなふうの終り方になってしまいました。
それはそれとしまして、前回の終わりのところで2進の浮動小数点計算について説明する、などということを書いてしまいました。
本当にそれを始めますと、またしてもAM188のシステムやKL5C80A12のシステムの開発作業に支障が出てしまいます。
それはちょっとテーマとして大きすぎました。
浮動小数点計算のシステムプログラムはそれだけで解説書が1冊書けてしまうくらいの内容があります。
入口だけでもとも考えたのですが、とても無理そうです。
ですので、それについてはいずれ時間をみつけて、ということでお許しください。
でも全然書かないわけにもいきませんので、今回は10進数がどのような形で2進数の浮動小数点数に変換されているのか、というあたりについて、まとまりがない説明ですが、とにかく書いてみることにしました。
今回の記事を書こうとして私自身が気がついたのですが、FOR〜NEXTの終了条件であるPI/2の値がちょっと雑ではないか、と少し気になりました。
前回のテスト画面でPI/2はA=1.5708になっています。
PIは3.14159265ですからその1/2は1.570796になります。
どうやらその末尾が四捨五入された結果1.5708になったようです。
うーん。
ちょっとアバウトかなあ。
そう思いましたので、前回のテストに関係する値について計算をしてみました。
比較のために、前回の記事の画面を開いた上にコマンドプロンプト画面を置きました。
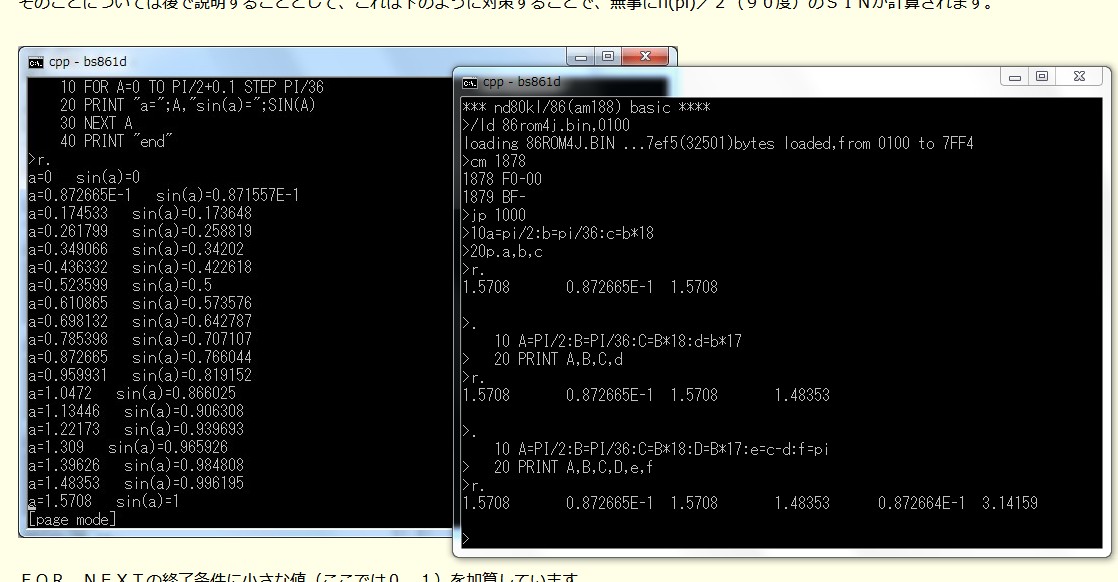
右の画面の一番下の計算では、PI/36に18を掛けたものからPI/36に17を掛けたものを引いています。
本当はFOR〜NEXTの場合には掛け算ではなくて加算の繰り返しですからもっと大きな誤差になります。
それはともかく、最後のステップで終了値(PI/2)との差が末尾1だけ小さくなっています。
刻み値が0.872665E−1なのに最後のところの差は0.872664E−1になっています。
言い換えれば、17回の繰り返しで、Aの値が末尾1だけ大きくなってしまったと言えます。
そこに最後の刻み値を加算するとPI/2よりも少しだけ大きくなってしまうので、そこでNEXTを抜け出してしまったと考えることができます。
さて。
上の右側の計算結果は実数型変数のA、B、C、D、E、Fに格納されています。
その値が格納されているメモリアドレスの内容をDMコマンドで表示させてみました。
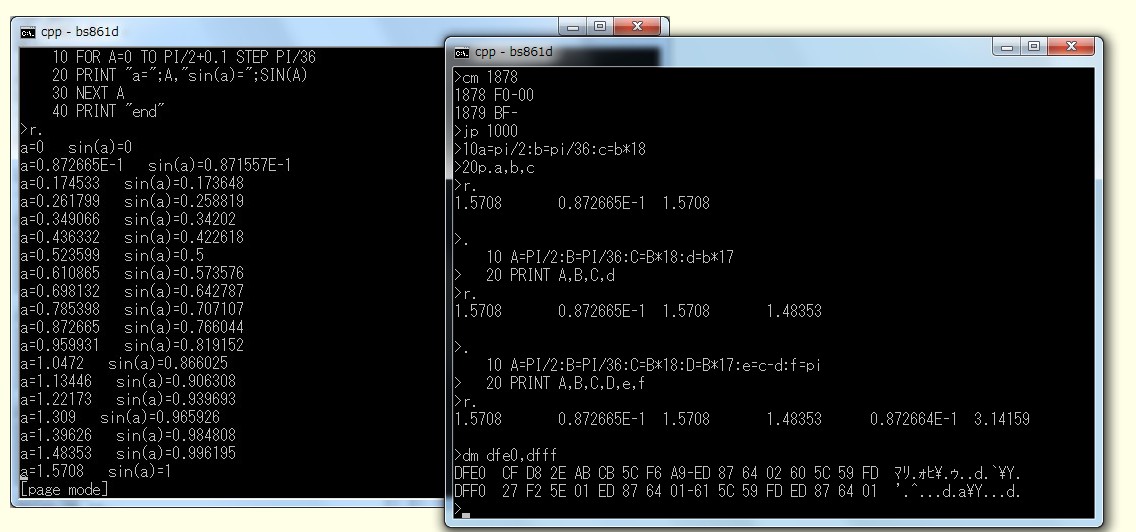
実数型変数は4バイトを占有します。
DFFFから前方に逆向きに格納されています。
これを普通の向きに直して整理すると下のようになります。
A 01 64 87 ED
B FD 59 5C 61
C 01 64 87 ED
D 01 5E F2 27
E FD 59 5C 60
F 02 64 87 ED
最初の1バイトは指数(符号付)です。
1バイト8ビットを使って−128〜+127を示します。
扱える数の大きさはここで決ります。
2〜4バイトは仮数部です。
最初の1ビットが符号(1のときマイナスを示す)で残り23ビットが2進数で表した数値になります。
AとCとFの仮数部が同じなのが分かりますでしょうか?
AとCはPI/2でFはPIです。
仮数部の左に小数点があるものとして考えてください。
AとCは指数が1ですから(.)6487ED×2です。
Fは指数が2ですから(.)6487ED×4です。
確かに1:2の関係になっていることはわかります。
この仮数部をどうしたら10進数に戻すことができるでしょうか?
それにはまず仮数部を整数値だと考えます。
左側に小数点があるということは、そのすぐ右の桁は小数第1位です。
10進数なら0.1(1/10)です。
2進数ですから1/2です。
その下は1/4、その下は1/8…です。
23ビットですから最下位は1/223です。
ということはもしも仮数部の数値を仮に小数点なしの整数だとしたら、実はその数を223で割ったものが真の値だということになります。
Windowsの電卓で計算をしてみましょう。
223は8388608です。
6487EDを10進数に直すと6588397になります。
6588397/8388608=0.7853981256…です。
これは仮数部の値です。
AとCはこの値に2を掛けます。
すると、1.570796…が得られます。
Fはそこにさらに2を掛けます。
すると、3.1415925…が得られました。
うーん。
なんだかわかったような、わからないような…。
うまく説明できませんが、まあこんなあたりでお許しください。
16ビットマイコンボードの製作[第37回]
2018.6.14upload
前へ
次へ
ホームページトップへ戻る