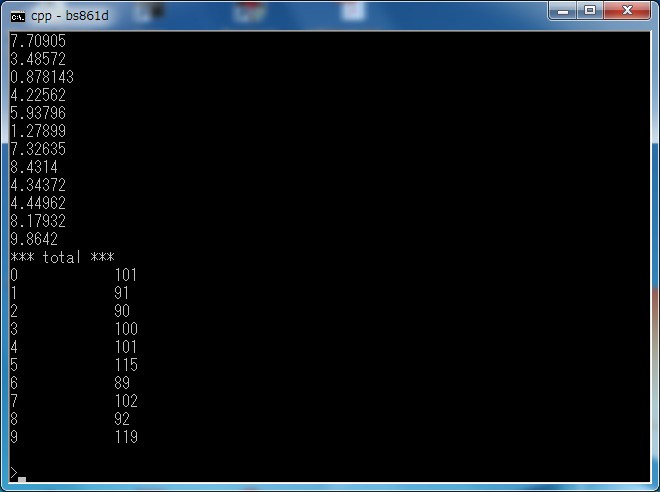
出力される数値も見たところランダムなようですし、0〜9に分けて集計した結果も大体同じぐらいの割合になっているようです。
これならよろしいのではありませんか?
16ビットマイコンボードの製作[第59回]
2018.7.19upload
2018.7.20訂正
前へ
次へ
ホームページトップへ戻る
16ビットマイコンボードの製作
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
いつか使ってみるつもりで入手してそのまま置いてあった16ビットCPUのことを思い出しました。
AMD社のAM188です。
その名の通り、CPUコアは80188互換の16ビットCPUです。
そのAM188を使った16ビットマイコンボードの製作記事です。
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
[第59回]
●RND関数/16bit Xorshift
RND関数はZB3BASICにも組み込まれています。
ただ正直なところ余り出来のよい関数ではありません。
せっかく16ビットの86版BASICを作るのですから、この機会にもう少しましな関数にしたいと考えていました。
RNDは乱数を発生する関数です。
マイコンのプログラムで乱数を発生させるアルゴリズムは昔から色々な方法が考えられてきました。
乱数発生法といえばすぐに思いつくのが平方採中法なのですが、古典過ぎていまどき使われることはないのだそうです。
そうするともう少しまともな乱数発生法は?
ということで例によってインターネットを検索したところ、M系列とかというものがみつかりました。
理論はよくわかりませんが、ソフトウェアとしてはそれほどむつかしいものではなさそうです。
なんでもビットシフトとXORを組み合わせるのだそうで、サンプルプログラムを参考にしてとりあえず組んでみたのですけれど。
これはだめですね。
乱数(マイコンなどで使うのは擬似乱数というものなのだそうですが)、その擬似乱数なるものの定義が私のイメージしているものとはちょっと異なっているようです。
私は乱数というからには、とにかく数値がランダムに発生して、その数値は前後の数値とは無関係に発生し、かつ発生割合が偏らないで一定のものというイメージでとらえていました。
よい例がサイコロです。
ところがM系列での乱数発生プログラムを試してみますと(私の理解が足りないためなのかも知れませんが)、どうやっても規則性が見えてしまいます。
なにかほかにもっとよい乱数発生法はないものか?
さらに検索を続けましたところ、おお、よいものがあるじゃありませんか。
それが今回のお題にありますXorshift法です。
Xorshiftとはどういうものなのか?
「Xorshift」で検索すると解説ページがたくさん見つかりますから、詳しくはそちらを参照してください。
Xorshiftはその名の通り、ビットシフトとXOR(排他的論理和)を組み合わせて計算を行ないます。
XORとビットシフトを組み合わせるところはM系列と同じですが、Xorshiftのほうはそれを多段に組み合わせます。
Wikipediaなどで解説されているものは32ビットの擬似乱数を発生させる例が多いのですが、ZB3BASICやそれをもとにした86版BASICの単精度浮動小数点計算で扱う実数の仮数部は符号付24ビットです。
正の数だけなら23ビットです。
どちらにしても32ビットの数は扱えません。
16ビットのXorshiftがあるとよいのですけれど。
さらに検索を続けてとうとうみつけました。
こちらのサイトにありました。
英文ですけれど。
16 bit xorshift rng(http://b2d-f9r.blogspot.com/2010/08/16-bit-xorshift-rng-now-with-more.html)
[2018.7.20訂正]リンク先が間違っていましたので訂正しました。
求めていた通りの16ビットのXorshiftですので、有難く使わせていただくことにいたしました。
下は同サイトを参考にさせていただいて(というかそのままですけれど)86BASICに組み込んだRND関数部分のプログラムリストです。
同サイトのXorshiftは16ビットの整数値を出力しますが、それを組み込んだ86BASICのRND関数は使い勝手を考えて0より大きくて1より小さい小数を出力します。
[00278] ;;;RND [00279] RND:;MOV CL,10 [00280] RND1:;MOV BL,03 [00281] RND2:;MOV DX,[RNDW] [00282] ;MOV AL,[RNDWH] [00283] ; [00284] 4082 50 PUSH AX [00285] 4083 53 PUSH BX [00286] 4084 51 PUSH CX [00287] 4085 52 PUSH DX [00288] 4086 A1DDF2 MOV AX,[RNDVLX] [00289] 4089 0BC0 OR AX,AX [00290] 408B 7503 JNZ RND3 <4090> [00291] 408D B80100 MOV AX,1 [00292] 4090 8BD0 RND3:MOV DX,AX [00293] 4092 B105 MOV CL,5 [00294] 4094 D3E2 SHL DX,CL [00295] 4096 33C2 XOR AX,DX [00296] 4098 8BD0 MOV DX,AX;t [00297] 409A B103 MOV CL,3 [00298] 409C D3EA SHR DX,CL [00299] 409E 33C2 XOR AX,DX [00300] 40A0 50 PUSH AX [00301] 40A1 A1DFF2 MOV AX,[RNDVLY] [00302] 40A4 0BC0 OR AX,AX [00303] 40A6 7503 JNZ RND4 <40AB> [00304] 40A8 B80100 MOV AX,1 [00305] 40AB A3DDF2 RND4:MOV [RNDVLX],AX [00306] 40AE 8BD0 MOV DX,AX [00307] 40B0 D1EA SHR DX [00308] 40B2 33C2 XOR AX,DX [00309] 40B4 5A POP DX [00310] 40B5 33C2 XOR AX,DX [00311] 40B7 A3DFF2 MOV [RNDVLY],AX [00312] 40BA 33D2 XOR DX,DX [00313] 40BC D1E8 SHR AX [00314] 40BE D1DA RCR DX [00315] ; [00316] 40C0 33DB XOR BX,BX [00317] 40C2 891EF7F1 MOV [*FA0],BX [00318] 40C6 881EF9F1 MOV [*FA2],BL [00319] 40CA 8916FAF1 MOV [*FA3],DX [00320] 40CE A3FCF1 MOV [*FA5],AX [00321] 40D1 891EFEF1 MOV [*FA7],BX [00322] ; [00323] 40D5 8A05 MOV AL,[DI] [00324] 40D7 3C23 CMP AL,23 ;# [00325] 40D9 7407 JZ DRND <40E2> [00326] 40DB 57 PUSH DI [00327] 40DC E88607 CALL FNORZ <4865> [00328] 40DF EB0690 JMP DRND2 <40E7> [00329] 40E2 47 DRND:INC DI [00330] 40E3 57 PUSH DI [00331] 40E4 E82E2C CALL DFNRZ <6D15> [00332] 40E7 5F DRND2:POP DI [00333] 40E8 5A POP DX [00334] 40E9 59 POP CX [00335] 40EA 5B POP BX [00336] 40EB 58 POP AX [00337] 40EC C3 RET |
そして下はRNDのテストプログラムと、その実行結果のログです。
RNDを呼ぶたびに得られる小数を10倍して、それを整数化することで、0〜9の出現率を集計します。
最初にテストのために作ったプログラムは100個の数を出力するものでしたが、ちょっと少ないので1000個に変更して実行しました。
1000個の数を出力しますので、ちょっと長くなりますから途中から後ろは省略しました。
>/load rndtst2.txt
10 DIM SUM(10)
20 FOR I%=0 TO 9
30 SUM(I%)=0
40 NEXT I%
50 FOR N%=0 TO 99
55 J=RND*10
60 J%=INT(J)
65 PRINT J
70 SUM(J%)=SUM(J%)+1
80 NEXT N%
85 PRINT "*** total ***"
90 FOR I%=0 TO 9
100 PRINT I%,SUM(I%)
110 NEXT I%
data end
> 50 FOR N%=0 TO 999
>r.
7.07764
9.8053
5.93018
3.31238
1.20117
7.70584
4.76547
1.45889
4.73282
8.5173
8.77045
0.967255
9.80164
5.2803
4.65729
1.34689
6.92184
5.35431
2.81769
8.2048
9.95605
0.228882E-1
1.49918
1.45706
7.53448
2.41745
8.91174
0.293732
4.10019
7.08206
5.9079
7.64908
8.62671
1.11252
3.64822
9.47983
3.90701
8.96988
4.3457
0.129547
|
こちらは最後の集計結果を表示している画面です。

出力される数値も見たところランダムなようですし、0〜9に分けて集計した結果も大体同じぐらいの割合になっているようです。
これならよろしいのではありませんか?
16ビットマイコンボードの製作[第59回]
2018.7.19upload
2018.7.20訂正
前へ
次へ
ホームページトップへ戻る