出力される数値も見たところランダムなようですし、0〜9に分けて集計した結果も大体同じぐらいの割合になっているようです。
16ビットマイコンボードの製作[第60回]
2018.7.22upload
前へ
次へ
ホームページトップへ戻る
16ビットマイコンボードの製作
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
いつか使ってみるつもりで入手してそのまま置いてあった16ビットCPUのことを思い出しました。
AMD社のAM188です。
その名の通り、CPUコアは80188互換の16ビットCPUです。
そのAM188を使った16ビットマイコンボードの製作記事です。
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
[第60回]
●倍精度RND#関数/32bit Xorshift
前回は単精度の浮動小数点計算プログラムに合わせるため、インターネットを検索してみつけたサイトから16bitのXorshiftを有難くいただいてRND関数として実装しました。
その際引用元のサイトを紹介しようとして、うっかり間違えて別のサイトを紹介してしまいました。
現在は正しいサイトのリンクに訂正済みです。
前回はXorshiftについて、ネットで紹介されているものの多くは32bit版なので、単精度浮動小数点計算プログラムには使えない、ということでネットをサーチして16bit版をみつけて組み込んだのでしたが、よく考えてみましたら、32bit版は倍精度浮動小数点計算プログラムには使えることに気が付きました。
倍精度浮動小数点計算では符号なし正の数は55bitまで扱えます。
それなら余裕で32bitのXorshiftを組み込むことができます。
32bitのXorshiftはWikipediaにも何例かが紹介されていますが、そのうちの最もシンプルなものを使わせていただくことにしました。
ただどうもWikipediaで紹介されているシフト回数(左13、右17、左15)はどうやらミスプリントのような気がします。
試してみたのですが、ちょっと数値に偏りが出るようです。
それで、こちらのサイトで紹介されていたシフト回数(左13、右17、左5)を使わせていただくことにしました。
こちらも英文ですけれど。
Xorshift RNGs for small systems(http://excamera.com/sphinx/article-xorshift.html)
下は同サイトを参考にさせていただいて86BASICに組み込んだ倍精度RND#関数部分のプログラムリストです。
今回のRND#関数も前回の単精度RND関数と同様、使い勝手を考えて0より大きくて1より小さい小数を出力します。
[00165] ;DRND=6D99 [00166] 6D99 50 PUSH AX [00167] 6D9A 53 PUSH BX [00168] 6D9B 51 PUSH CX [00169] 6D9C 52 PUSH DX [00170] 6D9D 56 PUSH SI [00171] 6D9E A1DDF2 MOV AX,[RNDVLX] [00172] 6DA1 0BC0 OR AX,AX [00173] 6DA3 750E JNZ DRND1 <6DB3> [00174] 6DA5 8B16DFF2 MOV DX,[RNDVLY] [00175] 6DA9 0BD2 OR DX,DX [00176] 6DAB 7506 JNZ DRND1 <6DB3> [00177] 6DAD B8A28C MOV AX,8CA2;=2463534242 [00178] 6DB0 BAD692 MOV DX,92D6 [00179] 6DB3 8BD8 DRND1:MOV BX,AX [00180] 6DB5 8BF2 MOV SI,DX [00181] 6DB7 B10D MOV CL,0D;=13 [00182] 6DB9 D1E0 DRND2:SHL AX [00183] 6DBB D1D2 RCL DX [00184] 6DBD E2FA LOOP DRND2 <6DB9> [00185] 6DBF 33C3 XOR AX,BX [00186] 6DC1 33D6 XOR DX,SI [00187] 6DC3 8BD8 MOV BX,AX [00188] 6DC5 8BF2 MOV SI,DX [00189] 6DC7 B111 MOV CL,11;=17 [00190] 6DC9 D1EA DRND3:SHR DX [00191] 6DCB D1D8 RCR AX [00192] 6DCD E2FA LOOP DRND3 <6DC9> [00193] 6DCF 33C3 XOR AX,BX [00194] 6DD1 33D6 XOR DX,SI [00195] 6DD3 8BD8 MOV BX,AX [00196] 6DD5 8BF2 MOV SI,DX [00197] 6DD7 B105 MOV CL,5 [00198] 6DD9 D1E0 DRND4:SHL AX [00199] 6DDB D1D2 RCL DX [00200] 6DDD E2FA LOOP DRND4 <6DD9> [00201] 6DDF 33C3 XOR AX,BX [00202] 6DE1 33D6 XOR DX,SI [00203] 6DE3 0BC0 OR AX,AX [00204] 6DE5 750A JNZ DRND5 <6DF1> [00205] 6DE7 0BD2 OR DX,DX [00206] 6DE9 7506 JNZ DRND5 <6DF1> [00207] 6DEB B8A28C MOV AX,8CA2;=2463534242 [00208] 6DEE BAD692 MOV DX,92D6 [00209] 6DF1 A3DDF2 DRND5:MOV [RNDVLX],AX [00210] 6DF4 8916DFF2 MOV [RNDVLY],DX [00211] 6DF8 D1EA SHR DX [00212] 6DFA D1D8 RCR AX [00213] ; [00214] 6DFC 33DB XOR BX,BX [00215] 6DFE 891EF7F1 MOV [*FAH0],BX [00216] 6E02 881EF9F1 MOV [*FAH2],BL [00217] 6E06 A3FAF1 MOV [*FAH3],AX [00218] 6E09 8916FCF1 MOV [*FAH5],DX [00219] 6E0D 891EFEF1 MOV [*FAH7],BX [00220] ; [00221] 6E11 57 PUSH DI [00222] 6E12 E8C702 CALL FNRZ <70DC> [00223] 6E15 5F POP DI [00224] 6E16 5E POP SI [00225] 6E17 5A POP DX [00226] 6E18 59 POP CX [00227] 6E19 5B POP BX [00228] 6E1A 58 POP AX [00229] 6E1B C3 RET |
そして下はRND#のテストプログラムと、その実行結果のログです。
RND#を呼ぶたびに得られる小数を10倍して、それを整数化することで、0〜9の出現率を集計します。
前回と同様に、最初にテストのために作ったプログラムは100個の数を出力するものでしたが、ちょっと少ないので1000個に変更して実行しました。
1000個の数を出力しますので、長くなりますから途中から後ろは省略しました。
>.
10 DIM SUM(10)
20 FOR I%=0 TO 9
30 SUM(I%)=0
40 NEXT I%
50 FOR N%=0 TO 99
55 J#=RND#*10
60 J%=INT(J#)
65 PRINT J#
70 SUM(J%)=SUM(J%)+1
80 NEXT N%
85 PRINT "*** total ***"
90 FOR I%=0 TO 9
100 PRINT I%,SUM(I%)
110 NEXT I%
> 50 FOR N%=0 TO 999
>r.
2.650548508390784
1.019630888476968
5.496233752928674
9.850675333291292
0.3015256021171808D-1
9.794000228866935
3.122008945792913
1.109533817507327
2.921380344778299
6.791556607931852
0.9356176573783159
2.082222597673535
6.927995583973825
6.918896185234189
1.417034310288727
1.495721628889441
9.912803852930665
6.350246015936136
4.80824975296855
9.270115941762924
0.8053133683279157
3.724904297851026
7.156409691087902
4.85046561807394
5.475174710154533
9.352885149419308
7.514114063233137
4.597803764045238
1.567883798852563
6.747597646899521
7.469460684806108
9.491493585519493
2.77332860045135
6.704114167951047
8.185763978399336
3.935285890474916
6.501082014292479
4.957326641306281
8.552479213103652
5.437393900938332
5.753735820762813
1.602707905694842
5.669019613415003
4.787343135103583
8.703863648697734
0.1203180523589253
5.309926080517471
0.2047484600916505
7.767739803530276
1.946398857980967
2.16327540576458
4.669739007949829
9.878313760273159
5.246990034356713
1.25498537439853
1.34437526576221
4.604878509417176
7.117380853742361
|
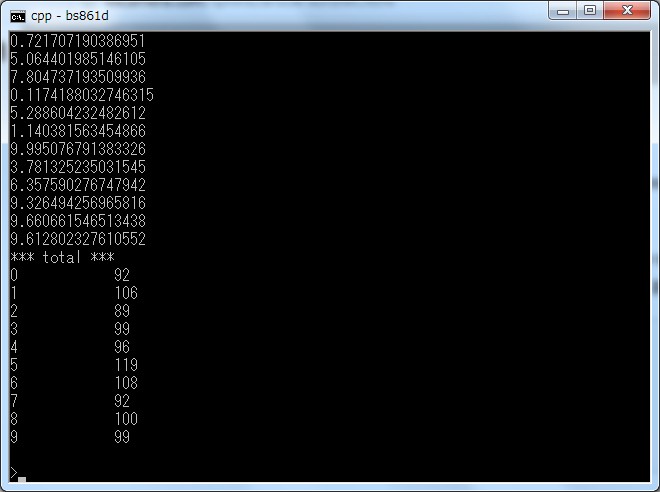
こちらは最後の集計結果を表示している画面です。

出力される数値も見たところランダムなようですし、0〜9に分けて集計した結果も大体同じぐらいの割合になっているようです。
16ビットマイコンボードの製作[第60回]
2018.7.22upload
前へ
次へ
ホームページトップへ戻る