標準TTLだけ(!)でCPUをつくろう!(組立てキットです!)
(ホントは74HC、CMOSなんだけど…)
[第133回]
●Full Adder回路
前回は下位桁からのキャリーを考慮しない加算回路(Half Adder)について説明しました。
Half Adder回路に、下位桁からのキャリーを入力する回路を付加したものが、Full Adder(全加算)回路です。
前回のHalf Adderの真理表にキャリー(C0)を付加した真理表を書いてみました。
| A1 |
B1 |
C0 |
Y1 |
C1 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
1 |
| 0 |
0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
1 |
1 |
表の上4行は下位桁からのキャリーが無い場合(C0=0)です。キャリーがありませんから、Half Adderと同じ結果になります。
下の4行はC=1で下位桁からのキャリーがある場合です。
この表を見ながら、1ビットのFull Adder回路について、考えてみます。
●Full Adder回路です
先に回路図をお見せしましょう。
Half Adder回路(破線の部分)に、下位桁からのキャリー入力(C0)を追加すると、Full Adder(全加算)回路になります。
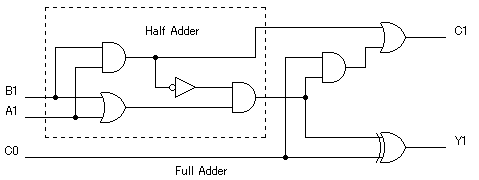
まずはキャリー出力C1について、考えてみます。
さきほどの真理表を見ながら考えてみましょう。
C0があっても、なくても、A1=1、B1=1のときはC1(上位桁へのキャリー)=1になります。
そのほかにも、A1+B1=1のときに下位桁からのキャリーが加われば(C0=1ならば)、やっぱり結果は2になるので、上位桁へのキャリーが発生します。
つまり、A1+B1=1で、かつC0=1のときにもC1=1になるわけですから、A1+B1の結果の出力(Half Adderの結果の出力)とC0のANDをとったものもC1=1になります。
この新たにできたC1への出力と、もとのHalf Adder回路からのキャリー出力のORがFull Adder回路のC1出力になります。
さて、結果の出力Y1のほうです。
理解を助けるために、Half Adderの出力(A1+B1の結果の出力)をY1’として、それとC0を入力としたときの、結果の出力Y1との関係を表にしてみました。
| A1 |
B1 |
Y1' |
C0 |
Y1 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
1 |
| 1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
1 |
0 |
| 1 |
1 |
0 |
1 |
1 |
Y1’とC0を2つの入力と考え、Y1をその出力として考えてみます。
すると、Y1’かC0のいずれか片方のみが1(他方は0)のときは結果のY1は1になり、両方とも0か、両方とも1の場合には、結果のY1は0になります。
入力が、1、0または0、1のときに結果が1になり、入力が0、0か1、1のときは結果が0になるのですから、これはXOR(排他的論理和)です。
代表的なXORゲートは74HC86です。
そこで、回路図のように、Half Adderからの出力(Y1’)とC0をXORゲートに入力すれば、その出力がY1になるのです。
じつはHalf Adder回路もXORを使えばもっと簡単になってしまいます。
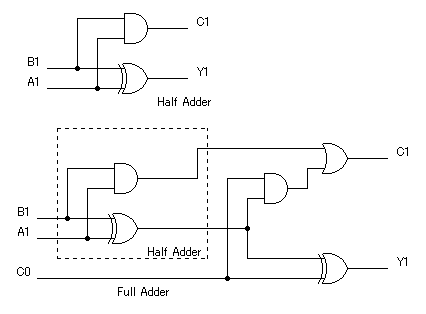
Half Adderならわずか2ゲートでできてしまいます。
前回も言いましたように、4ビットでも8ビットでも、この回路(Full Adder回路)をビットの数だけつなげば、多ビットのFull Adder回路になってしまいます。
●4ビットのFull Adder回路です
74HC283と同じ動作をする4ビットのFull Adder回路です。
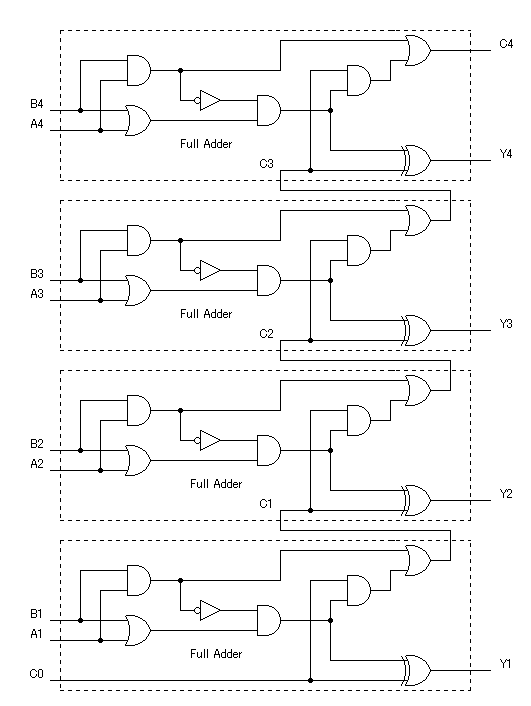
Half Adder部分はXORになっていませんが、それにはわけがあります。
もちろん、さきほどの説明のように、Half Adder部分にXORゲートを使っても全く構いません。
この回路図と74HC283の内部論理回路図とを比較し易くするために、XORを使わない表現のままにしておいたのです。
●74HC283の内部論理回路図です
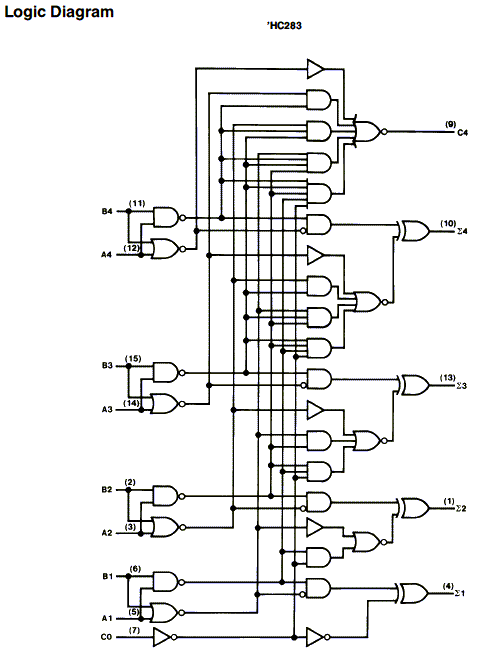
[出典]National Semiconductor社MM74HC283DataSheet
74HC283の内部ロジックも上でお見せした、4ビットのFull Adder回路と同じロジックで組み立てられています。
え?
違っているじゃないか、ですって?
同じなのですよ。
どこが違うかというと、上で説明したFull Adder回路は、中間のゲートの出力が正論理(AND、OR)になっていますが、74HC283では負論理(NAND、NOR)になっています。
正論理のほうが、考えがわかりやすい上に、特に今回の回路に限って言えば、正論理の回路のほうがずっとすっきりしたものになります。
そんなことはメーカーの技術者だって「百も承知」のはずです。
それをわざわざ複雑な回路にしているのには、何かわけがあるはずです。
多分製造上の理由かなにかがあって、負論理のほうが作りやすい、からなのかもしれません。
それはともかく、これで74HC283は「ブラックボックス」ではなくなりました。
これで、「つくるCPU」の加算回路に74HC283を、欲求不満になることなく、使うことができます。
2008.12.28upload
前へ
次へ
ホームページトップへ戻る



