標準TTLだけ(!)でCPUをつくろう!(組立てキットです!)
(ホントは74HC、CMOSなんだけど…)
[第132回]
●74HC283の真理表の説明です
あっというまにクリスマスが終わってしまいました。
それでは、落ち着いて何かができるか、といいますと、なんたって「師走」っていうくらいですから、もう、気ぜわしくてたまりません。
じきに大晦日です。
除夜の鐘をつきにいって(近くのお寺で、一回10円でつかせてくれるんですよ)、それでもう「あけましておめでとうございます」です。
なんだか、もう、あれこれ、書いている気分ではありませんね。
そんな状況ですから、当連載も、落ち着かず、細切れ状態で、年を越してしまいそうです。
で、細切れの続きです。
前回、4bit Full Adder74HC283の真理表の説明を予約いたしました。
74HC283の真理表は前回お見せしましたが、もう一度、再掲いたします。
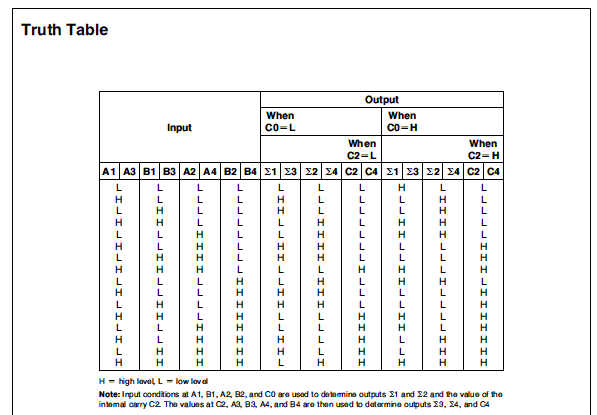
[出典]National Semiconductor社MM74HC283DataSheet
ちょっと見ただけでは、いったい何が書いてあるのか、よくわかりません。
この表は、本当は別々に書くところを、まとめてひとつにしてしまったものです。
A1、A3やB1、B3のように、ひとつの列に2つの端子名が書いてあります。
ここは
| A1 |
B1 |
A2 |
B2 |
(C0=Lの)Σ1 |
Σ2 |
C2 |
(C0=Hの)Σ1 |
Σ2 |
C2 |
と、
| A3 |
B3 |
A4 |
B4 |
(C2=Lの)Σ3 |
Σ4 |
C4 |
(C2=Hの)Σ3 |
Σ4 |
C4 |
の2つのグループの表をひとつにしてしまったものです。
この2つの表はまったく同じ値になるので、そのようにしてしまったのでしょう。
え?
やっぱり、わからない?
この表はA1〜A4の4ビットと、B1〜B4の4ビットを加算したときの、入力と出力の関係を示したものです。
A1〜A2+B1〜B2の下位2ビットどうしの加算と、A3〜A4+B3〜B4の上位2ビットの加算は、2ビットの計算として切り離せば同じことなので、そのような表になっているのです。
10進数の計算でも、たとえば1234+5678の計算は、桁上がりを考慮しなければ、12+56、34+78と2つに分けて計算することが可能で、その場合に、上位2桁と下位2桁の計算ルールは全く同じです。
ちなみに、その計算は、34+78=112、12+56=68で、下位からの繰り上がり(キャリー)を上位の結果に加算して、69と12を合体させた、6912が答えになります。
さきほどの表の前のグループは、A1〜A2+B1〜B2の下位2ビットの加算について、その下の桁からのキャリーがない場合(C0=L)とキャリーがある場合(C0=H)のそれぞれについて、計算結果の2ビット(Σ1、Σ2)と上位桁へのキャリー(C2)の値を示したものです。
後のグループは、A3〜A4+B3〜B4の上位2ビットの加算について、その下の桁からのキャリーがない場合(C2=L)とキャリーがある場合(C2=H)のそれぞれについて、計算結果の2ビット(Σ3、Σ4)と上位桁へのキャリー(C4)の値を示したものです。
計算のルールが同じなので、表の中身も同じになるのです。
●表のH、Lを1、0に置き換えてみます
表の意味はそういうことなのですが、でもやっぱり、よくわからない、かもしれません。
もう少し、わかりやすくしてみましょう。
すでに説明しましたように、下位2ビットの計算と、上位2ビットの計算は全く同じですから、下位2ビットについてだけ、考えてみます。
(本当は2ビットに分けないで、1ビットずつに分解して考えても、各ビットは同じになってしまうのですけれど、それについては、またあとで説明をいたします)
|
|
|
|
C0=0 |
|
|
C0=1 |
|
|
| A1 |
B1 |
A2 |
B2 |
Y1 |
Y2 |
C2 |
Y1 |
Y2 |
C2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
加算回路なのですから、このように、H、Lではなくて、1と0に置き換えたほうがわかりやすくなります。
この表をさらに、下のように並べ替えます。
|
|
|
|
C0=0 |
|
|
C0=1 |
|
|
| A1 |
A2 |
B1 |
B2 |
Y1 |
Y2 |
C2 |
Y1 |
Y2 |
C2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| 1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
| 0 |
+ |
0 |
= |
0 |
|
|
|
|
|
| 1 |
+ |
0 |
= |
1 |
|
|
|
|
|
| 0 |
+ |
1 |
= |
1 |
|
|
|
|
|
| 1 |
+ |
1 |
= |
2 |
|
|
|
|
|
| 2 |
+ |
0 |
= |
2 |
|
|
|
|
|
| 3 |
+ |
0 |
= |
3 |
|
|
|
|
|
| 2 |
+ |
1 |
= |
3 |
|
|
|
|
|
| 3 |
+ |
1 |
= |
4 |
(0+C) |
|
|
|
|
| 0 |
+ |
2 |
= |
2 |
|
|
|
|
|
| 1 |
+ |
2 |
= |
3 |
|
|
|
|
|
| 0 |
+ |
3 |
= |
3 |
|
|
|
|
|
| 1 |
+ |
3 |
= |
4 |
(0+C) |
|
|
|
|
| 2 |
+ |
2 |
= |
4 |
(0+C) |
|
|
|
|
| 3 |
+ |
2 |
= |
5 |
(1+C) |
|
|
|
|
| 2 |
+ |
3 |
= |
5 |
(1+C) |
|
|
|
|
| 3 |
+ |
3 |
= |
6 |
(2+C) |
|
|
|
|
A1、A2とB1、B2が隣同士になるように、並べ替えました。
AもBも2ビットですから、その組み合わせは、それぞれ、00、01、10、11の4通りです。これを10進数に直せば、0、1、2、3になります。
つまり、この表は0〜3+0〜3の計算の全ての場合を示しているのです。
表の下に上の各行の計算を10進数の計算に直したものをつけ加えました。
まずは下位桁からのキャリーがない場合(C0=0)について示してあります。
計算結果が3よりも大きくなると、上位桁への繰り上がり(キャリー、C2)が発生します。
表で、結果が4〜6のときは、その後ろに()で、結果の2ビットが、0〜2になって、キャリー(C)が発生することを、示しています。
次に同じことを、下位桁からのキャリーがある場合(C0=1)について示します。
計算結果はもとの表の右側(C0=H)の部分になります。
|
|
|
|
C0=0 |
|
|
C0=1 |
|
|
| A1 |
A2 |
B1 |
B2 |
Y1 |
Y2 |
C2 |
Y1 |
Y2 |
C2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| 1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
| 0 |
+ |
0 |
+ |
1 |
|
= |
1 |
|
|
| 1 |
+ |
0 |
+ |
1 |
|
= |
2 |
|
|
| 0 |
+ |
1 |
+ |
1 |
|
= |
2 |
|
|
| 1 |
+ |
1 |
+ |
1 |
|
= |
3 |
|
|
| 2 |
+ |
0 |
+ |
1 |
|
= |
3 |
|
|
| 3 |
+ |
0 |
+ |
1 |
|
= |
4 |
(0+C) |
|
| 2 |
+ |
1 |
+ |
1 |
|
= |
4 |
(0+C) |
|
| 3 |
+ |
1 |
+ |
1 |
|
= |
5 |
(1+C) |
|
| 0 |
+ |
2 |
+ |
1 |
|
= |
3 |
|
|
| 1 |
+ |
2 |
+ |
1 |
|
= |
4 |
(0+C) |
|
| 0 |
+ |
3 |
+ |
1 |
|
= |
4 |
(0+C) |
|
| 1 |
+ |
3 |
+ |
1 |
|
= |
5 |
(1+C) |
|
| 2 |
+ |
2 |
+ |
1 |
|
= |
5 |
(1+C) |
|
| 3 |
+ |
2 |
+ |
1 |
|
= |
6 |
(2+C) |
|
| 2 |
+ |
3 |
+ |
1 |
|
= |
6 |
(2+C) |
|
| 3 |
+ |
3 |
+ |
1 |
|
= |
7 |
(3+C) |
|
どちらの表も、いまひとつ、数の並びが面白くありません。
これは、もとの表が、A1、B1、A2、B2の並びになっていて、それを4ビットの入力信号として扱っているためです。
数の加算回路なのですけれど、ANDやORなどの論理回路と同じ扱いなのですね。
●じつは、論理回路なのです
というのも、このレベルでは、数値演算回路というよりも、論理演算回路といったほうがなじみやすいレベルなのです。
計算結果の表なのに、HとLを使って、真理表(Truth Table)などと表現しているのは、多分そういった意味合いからなのだと思われます。
そこで、そのあたりをもう少し掘り下げて、考えてみたいと思います。
●加算回路の論理的考察
なんて、格好つけてしまいました。
上の方で、「じつは1ビットに分解できる」と書きました。
そこで、まず、1ビットと1ビットの加算について考えてみます。
さきほどの表で、A1+B1=Σ1(とキャリー)のところだけ、抜き出してみます。
| A1 |
B1 |
C0 |
Y1 |
C1 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
1 |
まずは下位桁からのキャリーは無い場合(C0=0)について考えてみます。
C0が邪魔ですから、外してしまいましょう。
そうすると、こうなります。
| A1 |
B1 |
Y1 |
|
C1 |
| 0 |
0 |
0 |
|
0 |
| 1 |
0 |
1 |
|
0 |
| 0 |
1 |
1 |
|
0 |
| 1 |
1 |
0 |
|
1 |
この表って、どこかで見たような…。
ほら。
| A1 |
B1 |
Y1 |
|
C1 |
| 0 |
0 |
0 |
|
0 |
| 1 |
0 |
1 |
|
0 |
| 0 |
1 |
1 |
|
0 |
| 1 |
1 |
1 |
|
1 |
入力がA1とB1で出力がY1という、この表は?
そうです。2入力ORゲート(74HC32など)の真理表です。
あっと、残念。一番下だけ、結果が逆になっています。
でもよく、似ていますね。ORは日本語では、「論理和」といいます。やっぱり足し算なんですよ。
そして、C1に注目すると。
| A1 |
B1 |
Y1 |
|
C1 |
| 0 |
0 |
0 |
|
0 |
| 1 |
0 |
0 |
|
0 |
| 0 |
1 |
0 |
|
0 |
| 1 |
1 |
1 |
|
1 |
この表のY1が、C1と同じになっています。
では、この表は?
もう、わかりますよね。2入力ANDゲート(74HC08など)の真理表です。
すると、A1+B1=Y1+Cという回路は、みんながよく知っているゲートICで簡単に組めてしまうことがわかります。
はい。こういう回路になります。
●Half Adder回路
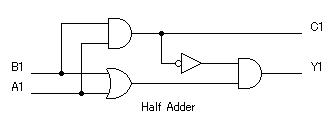
上位桁へのキャリー出力はありますが、下位桁からのキャリー入力はありません。ちょいと中途半端ですから、Half Adder(半加算)回路です。
キャリー出力はAND回路からの出力そのままです。
結果の出力Y1はOR回路の出力に近いのですが、残念ながら、A1=1、B1=1のときだけ結果が0になっていました。
A1=1、B1=1というのは、C1=1のときですから、ANDの出力を利用して、図のように、C1=1のときは、Y1=0になるようにしてやれば、上の真理表のとおりになります。
ほうら、加算回路なんて難しそうに思っていたかもしれませんけれど、わりと簡単な論理回路になってしまいましたでしょ?
さて、この次は、下位桁からのキャリーを含めた、Full Adder(全加算)回路の説明にいくわけなのですが、時間がなくなってしまいました。
この続きは、また次回にいたします。
2008.12.26upload
前へ
次へ
ホームページトップへ戻る

