DAAのお話の最終回、のつもりだったのですけれど、最後まで書いていったら、またもう1回、続きを次回書かねばならなくなってしまったようです…。
簡単に済ませるつもりだったのですが、大変なお話になってしまいました。
でも、このテーマについては、今回でやっとおしまいにできそうです(残念ながら、終わりません)。
なぜ、こんなに長いお話になってしまったかと言いますと、早い話が(全然、早くない!)、ただ単に私が要領良くまとめられなかったから、ということにつきます。
しかし、要領が悪い点は別にして、その他の意図も実はあるのです。
自慢のクソは犬も食わぬ、などという言葉があるくらいで、昔の人は自分のことを吹聴するのは最もはしたないことだと戒めてきました。
しかし、今や万事宣伝の世の中です。
桃李もの言わざれども下おのずから蹊を成す、なんて悠長なことを言っている時代ではないのですね。
私の作ったボードはこんなに優れてますよー、とか、このキットは開発するまでに、なんと、10年もかかったんです!
なんて宣伝をすると、
ほー、そんなにすごいキットなら、少し高いが、いちど買ってみるか、と言ってもらえるかもしれません。
あとで気がついたのですけれど、そうすると、これ、2ヶ月で開発したんです、なんて書くのは、アホだったのか、と…。
なんだ、たった、2ヶ月で作ったのか。そんなもん、どーせ、いいかげんなものにきまってるさ。
それにしては、ちょっと、高すぎるんじゃないのぉ?
うーん。こういうのを、後の祭、などと申します。
いまからでも、遅くはないかもしれないから、訪問者様が増えないうちに、書き直しておくか…。
2ヶ月っていうのは、間違いでした。じつは2年かかったんです…。
いくらなんでもそういう、見え見え、なこともいまさらできません。
せめて、できるとすると、
2ヶ月っていったって死ぬほどがんばった2ヶ月だったんですよぉ(これもなんだかウソくさい)。
でもまあ、これだけ中身が濃ーいのですよー、ということだけでも、ご理解いただければ、という意図もあって、しつこく書いているのです。
ひょっとすると、
これだけのことができるところならば、ひとつ、仕事を依頼してみようか?
などというお客様も来ていただけるかも、しれませんし、ね。
(そのようにお考えのお客様がもしいらっしゃいますなら、お電話、メールにてお問い合わせください。単品、小ロット、試作、いずれも承ります。個人、法人を問いませんが、ただ、それなりに費用がかかりますので、趣味目的で「カスタムオーダー」というのは無理かと思います)
今回、長々と書いてきた、DAAについてですが、いささか自画自賛になることをお許しいただいたとして、言わせていただければ、
たった1つのDAA命令に対しても、これだけ考えることがあったのですよ、
ということについては、「ガッテンして、いただけましたでしょうか?」。
例によって、ちょいとノートをお見せすることにいたします。

これは2008年5月24日〜5月25日のノートです。
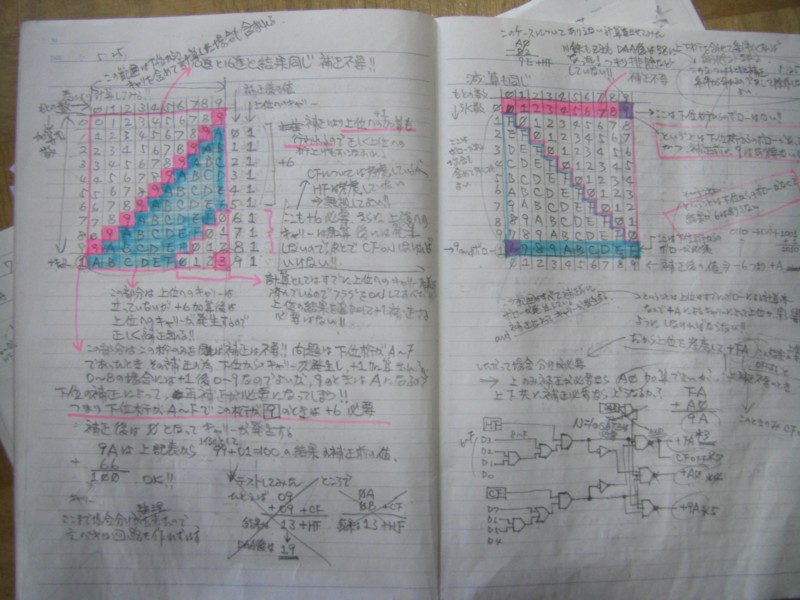
こちらも5月25日のノートです。
あれまあ、カレンダーで確認してみたら、日曜日、だったのですねぇ。
思い出しました。
この日は家族と一緒にアピタに買い物に来て、私は軽食コーナーの隅っこのテーブルで、コーヒーを飲みつつ、あたりをケシゴムのカスだらけにしながら、ノートと格闘していたのでした。
●それでは、どんな回路になるのでしょうか?
さて、余談は置くとして、今まで考えてきたことをまとめると、いったいどんな回路を考えたらよいのでしょうか?
今回の企画で、実際に設計した、DAA回路についても、ノートでお見せすることにいたします。
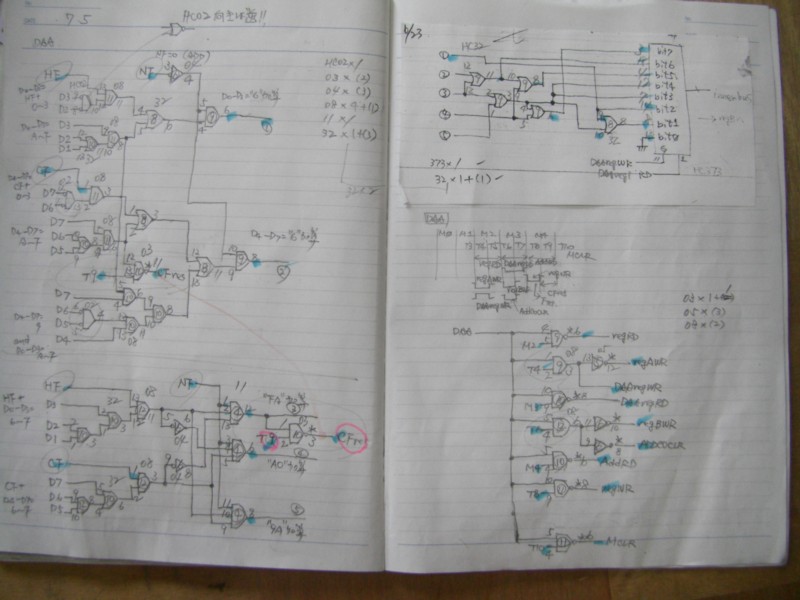
こちらは7月5日のノートです。
DAA回路については、5月に一度設計したのですが、気に入らなくて、その後6月23日に再度設計の見直しをしています。ノートの右上にそのときの回路の一部が貼り付けてあります。
最終的に7月5日付ノートの回路(上の写真)になりました。
まだ回路図の清書ができていませんから、お見せできるのは、これだけです。
このノートに描いた回路図をもとにして、基板パターン図はすでに作成済みです(ICナンバーと端子番号が記入済みであるのがわかります)。
まだ実際の基板も発注していませんし、そもそもそれ以前に、回路の最終確認作業も出来ていませんから、この回路でよいのかどうかはわかりません。基板作成と部品実装はまだかなり先になりそうです(DAAは優先順位が低いので、第3の基板になります)。
図も少し見難いかも知れませんね。お許しください。
なぜ、こういう回路になるのか、の説明は、とりあえず省略いたします(それをすると、余りに長くなってしまいます)。
この基板がもしキットとして世に出ることがあれば(多分、それは、無いでしょうけれど)、そのとき、回路の説明も添付したいと思います(ということは、この回路の説明をする日は永遠に来ないかも…)。
ノートの右頁中央にタイミングチャートが描いてあります(小さいので見難いとは思いますが)。
それを見ていただくと、この回路が普通のTTL回路ではなくてCPU回路なのだなぁ、と納得していただけるのでは、と思います(もちろん、DAAだけではなく、すべての命令の回路は、タイミングチャートに基づいて設計しています)。
回路のほとんどが2入力ゲートである、という点については、異論があろうか、と思います。
もう少し集積度の高いICを使えばICの数を減らせることができるのでは?というご指摘もあるかと思います。
ところが、残念ながら、普通に入手可能なTTLICでは、なかなか希望通りのものが無いのが現実です。CMOSの4000番シリーズならば便利なものもいろいろあるのですが、なにしろ、遅い!
純粋のトレーニング目的に限定するならば、ステップ動作さえできれば良いのですから、CMOSICを使うことも可能だと思いますが、そこはそれ、本物に近いものを、という思いも捨てきれなくて、CPUクロックは2MHz相当(マシンサイクルは0.5μsec)として回路動作を考えていることもあって、結果としてTTLのみの回路で、2入力のゲートICを多用することになりました(ちなみに、今回の回路のDAA命令のクロック数は5マシンクロックです。命令実行時間は2.5μsec)。
それに、とくに初心者にとっては、単純なゲートの組み合わせ回路の方がより理解しやすいのでは、とも思っています。
まあ、このあたりについては、試作から製品へ、という作業の流れの中で(そこまで続いていけば、の話ですけれど)、検討してみたいとも思っています。
できれば、汎用TTLだけで作りたい、というこだわりは、最後まで通したい、と思っているのですが…。
別のところでも、あらためて書くかもしれませんが、今回設計するにあたって、タイミングチャートを細部にわたって描いていく過程で感じたことは、TTLは遅い!ということでした。
CPUは確実な動作が命です。組立キットだからといって、そこのところをいいかげんな回路でごまかすわけにはいきません。
そう考えると、今回のキットの回路では、2MHzは多分限界だと思います(基板ができてきたら、クロックを上げて、4MHzでの動作テストをしてみたい、とは思っているのですが)。
じつは、ちょっとこわいなぁ、と内心思っているのは、全体の回路がバカでかくなってしまったことです。
回路の端から端までの配線長を考えると、2MHzでもあぶない、のでは?という不安があります。
まあ、これは、できてからの「お楽しみ」です。
TTLは意外に遅延時間が大きくて、たとえゲートでも段数が多くなると、その影響は無視できなくなります。
ほんとうに、大丈夫、でしょうか、ねえ?
●忘れてしまうところでした。Nフラグについてです
そもそも、DAAのお話を始めたきっかけは、Z80にはNフラグなるものがあるのに、8080にはそれが無かった(らしい)ということからでした。もう、すっかり忘れてしまうところでした。
今まで長々と説明してきましたが、その中で、
DAAの直前に行われた命令が加算命令であったときと、減算命令であったときとでは、補正の方法が異なっている、
ということがわかりました。
すると、当然のことながら、直前に行われたはずの命令が加算命令だったのか、減算命令だったのか、ということがわからなければ、補正のしようが無い、という道理になります。
補正前の2進数のどこにもそのような情報はありません。
今回の作業を始めるにあたって、当初手元に8080についての資料がまったく残っていないことがわかって困った、というお話をしました。必要な情報はインターネットから集めることができたのですが、命令の詳細な動作やフラグについては、Z80の資料をもとにして、設計をすすめました。
私はこのDAAについても何の疑問も感じずに、Z80の動作の通りに設計してしまったのです。
Z80にはNフラグがあって、加算命令を実行するとNフラグがリセットされ、減算命令が実行されるとNフラグがセットされます。
したがって、Nフラグさえ調べれば、直前に実行された命令が加算命令であったのか減算命令であったのかを知ることができます。
当然のことながら、私はこのNフラグを使って、DAA回路を設計したのです。
ところが、そのどこかの時点で、じつは、8080にはNフラグがなかったらしい、ということがわかってきました。
すると、8080の設計者は、Nフラグ無しで、どうやって、直前に行われた命令が加算命令だったのかそれとも減算命令だったのかを知ることができたのでしょうか?
うーん、わからん。これは、謎でした。
謎が解けたのは、TTLでCPUの組立キットをつくる、というこの記事を書き始めたとき、8080の命令コード表を参照させていただいた、半導体コレクション展示会場さまのページをあらためて再読していたときでした。
NECが、Intelの8080Aと同じ動作をする、として売り出したμPD8080Aに関する解説の以下のくだりを読んで、やっと疑問が解けました。
(NECのμPD8080Aは)減算のときにも10進補正命令が動作するという改良が(勝手に)行われていた石です。
(同ホームページから引用させていただきました)
そうか、8080のDAAは、減算に対する十進補正は行っていなかったんだ!
そういうことだったのです。
そんなことなら、Nフラグなど不要ですし、DAA回路ももっとシンプルになります。
せっかく減算に対する十進補正についても考えてしまった(!)ことですから、皆様にも長々と説明をしてしまいました。
回路図も描いてしまいましたから、これは参考回路として、何かの形で残したいとも考えています。
しかし、今回の試作基板については、基板発注までの間に、NフラグとDAAの減算後の十進補正回路は削除するように、作図変更を行うつもりです(だって、8080に無い機能だったわけですから、それに使用ICの数だって、少しでも減らしたいですから…)。
●負の2進数について、もう少し
前回、2進数の負数について、説明をしました。
もう少しだけ、説明が足りなかった点を補足したいと思います。
ここでこれから説明することは、いままで頭ではなく体で、いわば経験として覚えてきたことです。以下のように整理して考えてみたのは、じつは、今回が初めてです。
ところが、ところが、いざ説明を開始してみると、いやあ、これは!私自身が、おー、おー、という状態になってしまいました。
いまは惜しくも故人となってしまわれた、水野晴郎さんの名セリフを拝借して、
「いやぁ、コンピュータって、本当に面白いものですねぇ!」
と思わず言ってしまいたくなりました。
十進数の負数は、−12345というように、大きさを示す数値の前に−(負号)をつけて表します。
十進数の負数は、その大きさを絶対値としてとらえているようです。
十進数の負数に対して加算、減算を行うとその結果の数値は、正数に対する加算や減算を行ったときの結果の数値とは、数値そのものの(絶対値としての)増減が逆になります。
たとえば十進数の計算で、
正数の場合には加算は100+10=110、減算は100−10=90のようになりますが、
負数の場合には、加算は−100+10=−90、減算は−100−10=−110というように、計算結果を負号を外した絶対値で見てみると、正数の場合とは逆の増減をします。
このことは、たとえば正数については、貯金にさらに貯金を追加すれば、残高は増えるが、預金を引き出せば、残高は減る、と考え、
負数については、借入れに対して入金返済をすれば借入れ残高は減少するが、借入れがあるところにさらに借金をすれば借入れ残高は増える、と考えればつじつまが合います。
それでは、符号付の2進数の場合はどうなるのでしょうか。
上で説明した十進数の計算と同じ計算を行ってみます。
まず正数の加算です。100+10=110の計算を2進数(16進数)で行います。
0110 0100 100(16進数の64)
0000 1010(+ 10(16進数の0A)
0110 1110 110(16進数の6E)
次は正数の減算です。100−10=90の計算を2進数(16進数)で行います。
0110 0100 100(16進数の64)
0000 1010(− 10(16進数の0A)
0101 1010 90(16進数の5A)
続いて負数の加算です。−100+10=−90の計算を2進数(16進数)で行います。
1001 1100 −100(16進数の9C)
0000 1010(+ 10(16進数の0A)
1010 0110 −90(16進数のA6)
負数の減算です。−100−10=−110の計算を2進数(16進数)で行います。
1001 1100 −100(16進数の9C)
0000 1010(− 10(16進数の0A)
1001 0010 −110(16進数の92)
十進数の計算と2進数の計算では、もちろん結果は同じになりますけれど、こうやって比べてみると、十進数の負数と符号付2進数の負数とでは、決定的に違う(!)、あることに、気がつきませんか?
さて、それは、どういうことでしょうか?
(ヒントです。16進数の増減に注目してみてください)
ここで、その答えを書いて、その説明までしてしまうのは、いかにも、惜しい!
ということで、この続きは、次回にいたします。
2008.7.23upload
前へ
次へ
ホームページトップに戻る