昗弨俿俿俴偩偗乮両乯偱CPU傪偮偔傠偆両乮慻棫偰僉僢僩偱偡両乯
(儂儞僩偼俈係俫俠丄俠俵俷俽側傫偩偗偳乧乯
乵戞俇俆俋夞乶
仠儖乕僩寁嶼偺巇慻傒
偙偺偲偙傠丄俿俲亅俉侽梡偵彂偐傟偨儖乕僩寁嶼僾儘僌儔儉偵偮偄偰愢柧傪偟偰偍傝傑偡丅
俶俢俉侽倅嘨慻棫僉僢僩傪偛峸擖偄偨偩偄偨杒奀摴偺俵條偐傜丄俿俲亅俉侽墳梡僾儘僌儔儉偲偟偰憲偭偰偄偨偩偄偨僾儘僌儔儉偱偡丅
侽侾乣俋俋偺斖埻偺惍悢偺傒偱偡偑丄儖乕僩乮暯曽崻乯傪媮傔傞僾儘僌儔儉偱偡丅
侾俋俈俈擭摉帪偺嶨帍乽儅僀僐儞乿偵嵹偭偰偄偨婰帠傪傕偲偵丄俵條偑俴俤俢昞帵晹暘偵夵椙傪壛偊傜傟偨傕偺偩偲偄偆偙偲偱偡丅
巹偼攞惛搙偺晜摦彫悢揰墘嶼婡擻傪傕偮倅俛俁俛俙俽俬俠傪嶌傝傑偟偨偺偱倅俉侽偱儖乕僩偺寁嶼傪偝偣傞僾儘僌儔儉傕彂偔偙偲偑偱偒傑偡乮偲偄偄傑偟偰傕丄傕偆偢偄傇傫愄偵嶌偭偨傕偺偱偡偐傜丄傎偲傫偳婰壇偵偁傝傑偣傫偑乯丅
晜摦彫悢揰偺墘嶼偼俀恑悢偱峴側偄傑偡偟丄偐側傝暋嶨側僒僽儖乕僠儞孮偐傜峔惉偝傟偰偄傑偡丅
摉慠偺偙偲側偑傜丄僴儞僪傾僙儞僽儖偱偱偒傞傛偆側戙暔偱偼偁傝傑偣傫丅傾僙儞僽儔偑昁恵偵側傝傑偡丅
偱偡偐傜丄俵條偐傜僾儘僌儔儉傪儊乕儖揧晅偱憲偭偰偄偨偩偄偨偲偒丄偦偺梋傝偺抁偝偵丄嬃偒傑偟偨偟丄戝偄偵媈栤偱傕偁傝傑偟偨丅
偨偲偊嵟戝俀寘偺惍悢偵懳偡傞暯曽崻偵尷傞丄偲偄偆惂栺晅偒偱偁偭偨偲偟偰傕丄偙傟偼梋傝偵抁偡偓傑偡丅
偪傚偭偲怣偠傜傟側偄婥帩偪偱偟偨丅
偄偭偨偄偳偆傗偭偰寁嶼傪偟偰偄傞偺偩傠偆丄偲嫽枴捗乆偱丄偍憲傝偄偨偩偄偨僾儘僌儔儉傪夝愅偟偰傒傞偙偲偵偄偨偟傑偟偨丅
偍憲傝偄偨偩偄偨偺偼儅僔儞岅偺僶僀僫儕僼傽僀儖偱偟偨偐傜丄偦偺傑傑偱偼側偐側偐夝撉偡傞偙偲偑崲擄偱偡丅
偦偙偱俶俢俉侽倅嘨慻棫僉僢僩偵娷傑傟偰偄傞丄倅俉侽媡傾僙儞僽儔丄倅俉侽傾僙儞僽儔側偳偺僣乕儖傪巊偭偰丄儖乕僩寁嶼僾儘僌儔儉傪棟夝偟傗偡偄宍偵曇廤偟側偍偟傑偟偨丅
偲偄偆偲偙傠傑偱偑丄慜夞傑偱偺偍榖偱偡丅
崱夞偼偄傛偄傛丄偦偺儖乕僩寁嶼偺旈枾偵偣傑傝傑偡丅
乮側傫偩偐朸斣慻偺僉儊僙儕僼偺傛偆偱偡乯
儖乕僩偺寁嶼傪峴側偭偰偄傞偺偼僾儘僌儔儉偺丄埲壓偺晹暘偱偡丅
怣偠傜傟側偄傎偳娙扨偱偡丅
;
;KEISAN START
;
8023 3E01 LD A,01
8025 32B382 LD (HIKUSU78),A
8028 CD7080 KEISAN_LOOP:CALL HIKIZAN
802B DA3780 JP C,KEISAN_END
802E CD8480 CALL KOTAE_ADD1
8031 CD9380 CALL HIKUSUADD2
8034 C32880 JP KEISAN_LOOP
傛偔尒傑偡偲俁偮偺僒僽儖乕僠儞傪俠俙俴俴偟偰偄傑偡丅
俫俬俲俬倅俙俶偲俲俷俿俙俤丵俙俢俢侾偲俫俬俲倀俽倀俙俢俢俀偱偡丅
嵟屻偺俫俬俲倀俽倀俙俢俢俀偼慜夞傑偱暋悢夞偵傢偨偭偰愢柧傪偟偰偒傑偟偨丅
傑偢偼偦傟偧傟偺僒僽儖乕僠儞傪帵偟偨偆偊偱愢柧傪偡傞偙偲偵偄偨偟傑偡丅
嵟弶偼俫俬俲俬倅俙俶偱偡丅
;
;TISU=TISU-HIKUSU
;
8070 21B382 HIKIZAN:LD HL,HIKUSU78
8073 11AF82 LD DE,TISU78
8076 0604 LD B,04
8078 AF XOR A
8079 1A HIKIZAN_2:LD A,(DE)
807A 9E SBC A,(HL)
807B 27 DAA
807C 12 LD (DE),A
807D 2B DEC HL
807E 1B DEC DE
807F 05 DEC B
8080 C27980 JP NZ,HIKIZAN_2
8083 C9 RET
偦偺柤偺捠傝丄抲悢偐傜堷偔悢傪尭嶼偡傞僒僽儖乕僠儞偱偡丅
抲悢乮俿俬俽倀侾俀乣俿俬俽倀俈俉乯丄堷偔悢乮俫俬俲倀俽倀侾俀乣俫俬俲倀俽倀俈俉乯偲摎偊乮俲俷俿俙俤侾俀丄俲俷俿俙俤俁係乯偼丄俼俙俵忋偵抲偐傟偰偍傝丄楢懕偟偨傾僪儗僗偵攝抲偝傟偰偄傑偡偑丄偦傟傪壓恾偺傛偆偵暲傋傞偲棟夝偟傗偡偔側傝傑偡丅
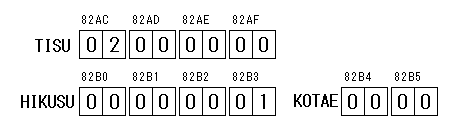
奺儗僕僗僞偺抣偼丄抲悢傪侽俀偲偟偰僗僞乕僩偟偨偲偒偺寁嶼奐巒捈慜偺抣偱偡丅
偙傟偐傜俀偺暯曽崻傪媮傔傛偆偲偟偰偄傑偡丅
抲悢偼侽侽乣俋俋偺惍悢俀寘偺斖埻偺悢偱丄忋偺恾偺傛偆偵丄廫恑俉寘偺儗僕僗僞偺忋埵俀寘偵抲偒傑偡丅
壓埵俇寘偼慡偰侽偑抲偐傟傑偡丅
堷偔悢偼恾偺傛偆偵弶婜抣侾偐傜僗僞乕僩偟傑偡丅偙偙傕廫恑俉寘偱偡丅
寁嶼寢壥偼摎偊乮俲俷俿俙俤乯偵廫恑係寘偱擖傟傜傟傑偡丅
寁嶼偼侾僶僀僩傪俀寘偺廫恑悢偱帵偡俛俠俢乮俀恑壔廫恑乯悢偲偟偰峴側傢傟傑偡丅
俛俠俢悢偵偮偄偰偼乵戞侾侽夞乶偱愢柧傪偟偰偍傝傑偡丅
寁嶼偼慡偰廫恑悢偺惍悢偲偟偰峴側傢傟傑偡丅
俫俬俲俬倅俙俶僒僽儖乕僠儞偱偼丄忋恾椺偺応崌丄
俀侽侽侽侽侽侽亅侾偺寁嶼偑峴側傢傟傑偡偑丄幚嵺偵偼俀侽侽侽侽侽侽偱偼側偔偰俀側偺偱偡偐傜丄俀丏侽侽侽侽侽侽亅侽丏侽侽侽侽侽侾偺寁嶼傪偟偰偄傞偙偲偵側傝傑偡丅
偟偐偟屌掕彫悢揰偺寁嶼偱偡偐傜丄彫悢揰傪庢偭偰偟傑偭偰丄惍悢摨巑偺寁嶼偲峫偊偰傕峔偄傑偣傫丅
偮偄偱偵摎偊乮俲俷俿俙俤乯偼惍悢係寘偱媮傔傜傟傑偡偑丄偙偙偼幚嵺偵偼丄侽丏侽侽侽偺埵抲偵彫悢揰偑偁傞偺偱偡偑丄偦傟偑徣棯偝傟偰偄傞偲峫偊偰偔偩偝偄丅
偦偺傛偆偵丄俫俬俲俬倅俙俶僒僽儖乕僠儞偼俿俬俽倀偐傜俫俬俲倀俽倀傪堷偄偰丄偦偺寢壥傪俿俬俽倀偵擖傟傑偡丅
師偼俲俷俿俙俤丵俙俢俢侾僒僽儖乕僠儞偱偡丅
;
;KOTAE_ADD1
;
8084 21B582 KOTAE_ADD1:LD HL,KOTAE34
8087 7E LD A,(HL)
8088 C601 ADD A,01
808A 27 DAA
808B 77 LD (HL),A
808C 2B DEC HL
808D 7E LD A,(HL)
808E CE00 ADC A,00
8090 27 DAA
8091 77 LD (HL),A
8092 C9 RET
偙傟傕娙扨側僾儘僌儔儉偱偡丅
俫俬俲俬倅俙俶僒僽儖乕僠儞偑侾夞幚峴偝傟傞搙偵丄摎偊乮俲俷俿俙俤乯儗僕僗僞偺抣傪亄侾偟傑偡丅
偮傑傝摎偊偼丄堷偒嶼傪偟偨夞悢偲摨偠偙偲偵側傝傑偡丅
偊丠
暯曽崻偑丄堷偒嶼傪偟偨夞悢偲摨偠丠
偦傟偼傑偨偳偆偄偆偙偲偱偟傚偆丠
偪傚偭偲怣偠傜傟傑偣傫丅
僇僊偼俫俬俲倀俽倀俙俢俢俀僒僽儖乕僠儞偵偁傝傑偡丅
;
; HIKUSU=HIKUSU+2
;
8093 0603 HIKUSUADD2:LD B,03
8095 21B382 LD HL,HIKUSU78
8098 7E LD A,(HL)
8099 C602 ADD A,02
809B 27 DAA
809C 77 LD (HL),A
809D 2B HIKUSUADD2_2:DEC HL
809E 7E LD A,(HL)
809F CE00 ADC A,00
80A1 27 DAA
80A2 77 LD (HL),A
80A3 05 DEC B
80A4 C29D80 JP NZ,HIKUSUADD2_2
80A7 C9 RET
偙偺僒僽儖乕僠儞偼堷偔悢乮俫俬俲倀俽倀乯儗僕僗僞偺抣偵俀傪壛偊傑偡丅
偨偩偦傟偩偗偱偡丅
偙偺俫俬俲倀俽倀俙俢俢俀僒僽儖乕僠儞傕丄俫俬俲俬倅俙俶僒僽儖乕僠儞偑侾夞幚峴偝傟偨偁偲偵丄摨偠傛偆偵侾夞幚峴偝傟傑偡丅
偡傞偲丄堦懱偳偆偄偆寁嶼傪偟偰偄傞偙偲偵側傞偱偟傚偆偐丅
嵟弶偵侽俀侽侽侽侽侽侽亅侾亖侽侾俋俋俋俋俋俋偑寁嶼偝傟丄偦偟偰俲俷俿俙俤偼侽亄侾亖侾偵側傝丄偦偟偰俫俬俲倀俽倀偼侾亄俀亖俁偵側傝傑偡丅
偦傟偱侾夞偺寁嶼偑廔傢傝傑偟偨丅
師偼丄俿俬俽倀偼侽侾俋俋俋俋俋俋亅俁亖侽侾俋俋俋俋俋俇丄俲俷俿俙俤偼侾亄侾亖俀丄俫俬俲倀俽倀偼俁亄俀亖俆偵側傝傑偡丅
偦偺師偼丄俿俬俽倀偼侽侾俋俋俋俋俋俇亅俆亖侽侾俋俋俋俋俋侾丄俲俷俿俙俤偼俀亄侾亖俁丄俫俬俲倀俽倀偼俆亄俀亖俈偵側傝傑偡丅
偦偺傛偆偵偳傫偳傫寁嶼偟偰偄偭偰丄嵟屻偵俿俬俽倀偐傜俫俬俲倀俽倀偑堷偗側偔側偭偨傜丄寁嶼廔椆偱丄偦偺偲偒偵俲俷俿俙俤偼俀偺暯曽崻偵側偭偰偄傞丄偲偄偆偺偱偡偗傟偳乧丅
偆偆偆丅
傎傫傑偐偄側偁丠
傑傞偱庤昳傪尒偣傜傟偰偄傞傛偆偱偡丅
傓丠
偱傕丄傑偰傛丠
偡傞偲丄堷偔悢偼丄侾丄俁丄俆丄俈丄俋乧偲偄偆悢楍偵側傞偺偱偼丠
傓傓丅側傫偩偐偼傞偐墦偄愄偵悢妛偺帋尡偵弌偰偒偨傛偆側乧丠
偦偟偰丄摎偊偺暯曽崻偲偄偆偺偑丄堷偒嶼傪偟偨夞悢偲偄偆偙偲偼乧丅
偦傟偼丄偮傑傝丄侾丄俁丄俆丄俈丄俋乧偺悢楍偺梫慺偺悢偲摨偠偱偼丠
偍偍丄傂傚偭偲偡傞偲丄偦傟側傜偽乧丅
崱丄媮傔傞摎偊偱偁傞暯曽崻丄偮傑傝堷偒嶼偺夞悢傪俶偲偡傞偲丄偦傟偼侾丄俁丄俆丄俈丄俋乧偺悢楍偺梫慺偺悢偲堦抳偟傑偡丅
俿俬俽倀偐傜丄堷偒偒傟側偔側傞傑偱丄偦偺悢楍傪弴偵堷偄偰偄偔偺偱偡偐傜丄偦偺悢楍偺憤榓偼俿俬俽倀偲摍偟偄偲峫偊傞偙偲偑偱偒傑偡乮抂悢丄偮傑傝梋傝偼愗傝幪偰偱偡乯丅
偱偼俶屄偺梫慺偐傜側傞悢楍侾丄俁丄俆丄乧丄俀俶亅侾偺憤榓偼偄偔偮偵側傞偱偟傚偆偐丠
偙傟丅愄偼彫妛峑偺嶼悢偱廗偭偨傫偱偡傛偹偊丅
栜榑俶側傫偰弌偰偒傑偣傫偟丄侾丄俀丄俁丄乧丄侾侽偔傜偄偺傕偺偱偟偨偗偳丅
乮弶傔偺悢亄廔傢傝偺悢乯亊屄悢亐俀
巚偄弌偟傑偣傫偐丠
偮傑傝憤榓俽亖乮侾亄俀俶亅侾乯亊俶乛俀
偱偡偐傜俽亖俶俀
偁傟傑丅偙傫側偲偙傠偵俀忔偑弌偰棃偰偟傑偄傑偟偨丅
悢楍偺憤榓俽偼抲悢偲摨偠丄偲偄偆偙偲偱偟偨偐傜丄偍偍丄妋偐偵丄俶偼抲悢俽偺暯曽崻偵側傞偠傖偁傝傑偣傫偐両
偄傗偁丄偙傟偼偡偛偄丅
嵟弶偵偳側偨偑偙偆偄偆偙偲傪巚偄偮偐傟偨偺偱偟傚偆丅
巹偼僾儘僌儔儉傪夝愅偡傞偙偲偵傛偭偰丄偦偺傛偆偵寁嶼偡傟偽傛偄丄偲偄偆寢榑偵偨偳傝偮偄偨傢偗偱偡偗傟偳丄偙傝傖偁偪傚偭偲巚偄偮偒傑偣傫傛偹偊丅
偦偆偟傑偟偨傜丄俵條偐傜偙傫側儁乕僕傪偛徯夘偄偨偩偒傑偟偨丅
http://www.wizforest.com/gear/tiger/sqrt/
側傞傎偳両擺摼偱偡丅
俀侽侾侽丏侾侾丏侾俀倳倫倢倧倎倓
慜傊
師傊
儂乕儉儁乕僕僩僢僾傊栠傞
