超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第61回]
●最良近似式について(2)
このところ本来のテーマから離れて、ずっと最良近似式について書いております。
途中休み休みではありますが、かれこれ1ヶ月以上も脱線したままです。
MYCPU80、CP/Mといったテーマに興味をもたれて、当サイトをご訪問いただいた方の中には「なんともしょーもないつまらぬことを書いておるではないか、いいかげんにしてはよ本題に戻らんかいな」、とお思いの方もおいでかも。
まことにごもっともであります。
が。
ときどき書いておりますように、当ブログ風記事は、そのまま私自身の備忘録をも兼ねております関係上、ときどきテーマ違いの脱線状態になってしまうことがあります。
このところちょっとしつこく近似式にこだわっておりますのは、私自身にとって最良近似式なるものは、二十数年来の未解決の疑問だったからです。
[第42回]に書いておりますように、二十数年前に「数値計算」(赤坂隆著。コロナ社刊)に記載の近似式を使ってBASICの初等関数のプログラムとして組み込んだものの、その近似式がどのようにして導き出されたものかは、当時は全く理解できませんでした。
今読めばその方法は同書中にしっかり説明されていたのでありますが、浅学菲才の悲しさ、当然のことながら理解不能のまま今日に至ってしまいました。
いえ。
その間ずっとそれを疑問に思っていたわけではありません。
ずっと都合よくすっかり忘れてしまっておりましたが、ここへきまして事の成り行きでこういうことに相成ってしまいました。
ま。しかし、お蔭様にて当時は全くちんぷんかんぷんでありました最良近似式につきまして、やっと一応の理解を得るところまでくることができました。
が。
このまま放っておきますと、せっかく理解できたものも、そのうちまたさっぱりわけわかめ状態に戻ってしまうのは必至であります。
ここは、忘れてしまう前に何としても書き留めておかねばならぬのであります。
という次第でありますので、今しばらくご辛抱いただき、お付き合いをばお願い申し上げます。
さて前回はその前の回からの疑問について一応の決着がついたのでありますが。
実はまだ他にも2つ3つ疑問が残っておりました。
ひとつはかなり根本的なことです。
このところ書いてきております最良近似式の求め方は、チェビシェフの近似式を元にしまして、その誤差の式
E(x)=y(x)−g(x)
に着目することで、徐々に真の最良近似式に至るという方法です。
y(x)は目的とする関数でg(x)はその近似式、E(x)は両者の差の関数です。
ここで問題になるのはy(x)はどこからもってくるのか、ということです。
このところ書いております近似式はsin(x)についてのものですから、当然y(x)=sin(x)ということになります。
昔ならば三角関数表がその根拠になりますでしょう。
しかしそれは大変な計算を覚悟しなければなりません。
幸い今はEXCELを利用することができます。
EXCELには関数sin(x)が内蔵されています。
で。疑問は?
EXCELのsin(x)も近似式なのでは?
というものです。
うーん。
これはその内容によりましては、以後の計算が全く根拠を失ってしまう可能性があります。
が。
そこに首をつっこんでしまいますと、藪の中に迷いこんでしまいそうです。
ここは素直に、なんたってMicrosoft様のEXCELでありますから、限りなく正確なsin(x)である、と信じてしまうことにいたしました。
ま。
そうではなかったとしましても、最良近似式の求め方自体が違ってくるわけではありませんから、とりあえずはそういうことにしておいてもよろしいでありましょう。
いまひとつの疑問でありますが。
それは計算誤差の問題です。
私はこのところの最良近似式を求める計算については、もっぱらEXCELを使って、特にその計算誤差を意識しないで強引に計算を行なってきました。
果たしてそれでよいのか?
という疑問です。
存在するであろう計算誤差による限界については目をつぶって、強引に計算した結果、一定の近似式を得ることができましたが、はたしてこの「最良近似式」は本当に「最良近似式」と言えるでありましょうか?
これも難しい問題です。
私には本当のところがどうなのかはよくわかりません。
ただ、一応EXCELのsin(x)がきわめて正確なものと仮定しまして、計算の結果導き出した最良近似式との差が一定の誤差の範囲にある、ということも同時に算出できていますから、「その誤差の範囲において最良な近似式」である、と考えてもよいのでは、と思います。
おお。
今頃になって、やっと気が付きました。
確かEXCELはセルの書式で数値の表示桁数を指定することができたはずでありました。
さっそくそのようにしてみました。
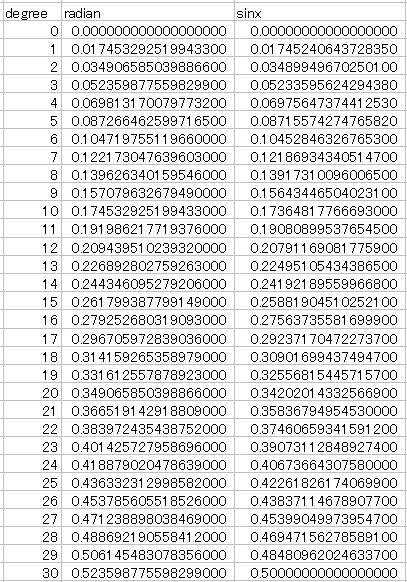
これを見ますとどうやらEXCELは有効数字15桁のようです。
それならば。
こちらはどうでしょう。
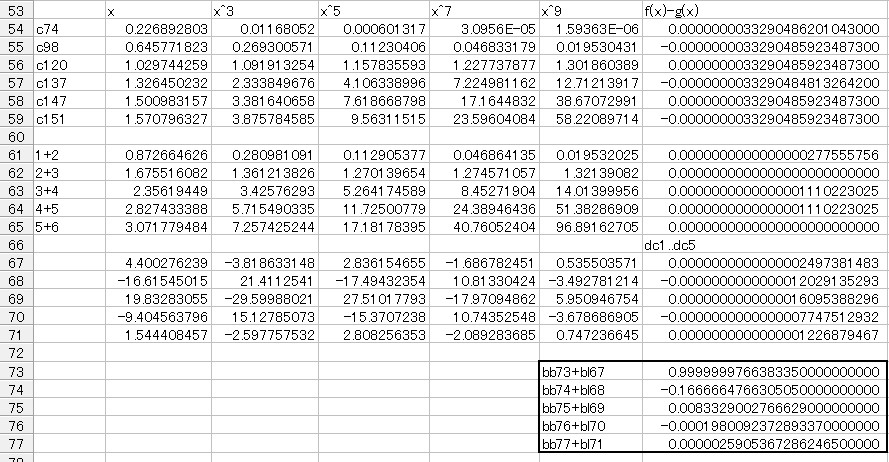
これはEXCELで連立方程式を解いて最良近似式の係数を求めているところです。
73行〜77行が計算によって求めた係数です。
こちらも有効数字15桁のようです。
もっとも有効数字が15桁だからといって、15桁の計算精度が保証されているということには全くならないのですけれど。
因みに上図の計算が正しいと仮定した場合、この最良近似式の誤差は最大で0.333×10−8になります(それは上図の54行〜59行の右端に表示されています)。
さて、まだもうひとつ疑問があります。
ですが、それにつきましては、説明の都合上、次回以降にて最良近似式の求め方について説明をした後にしたいと思います。
MYCPU80でCP/Mを![第61回]
2014.11.2upload
前へ
次へ
ホームページトップへ戻る