超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第60回]
●最良近似式に至る途中のグラフ(2)
前回、系列7の振幅が急に大きくなっているのがちょっと気になるので、計算ミスをしていないかどうか調べてみることにします、と書きました。
調べてみたのですが、計算におかしなところはありませんでした。
それともうひとつ、前回は計算の範囲を最初は60°から1°刻みで広げ、次に2°刻みで広げて、試しに計算を行い、最終的には5°刻みで90°までの範囲に徐々に広げて計算をおこなったのですが、そのように小刻みに計算を進めた場合と、荒く範囲を広げていった場合とで計算結果が異なってくるかどうかについては検証していません、と書きました。
それについても検証してみることにしました。
いっそのこと最初から範囲を0°から90°の全範囲として計算をしてみることにいたしました。
チェビシェフの近似式(9次の式)は60°近くまでは、その誤差のグラフは最良近似式に近い形をしていますが60°を越えるあたりから誤差が急に増大していきますから、最初からその全範囲を計算の対象とすることは無謀なことだと、私は考えていました。
しかし今回最初から全範囲を対象に計算をしてみて、それが私の思い違いであったことがわかりました。
下がそのようにしてチェビシェフの近似式をもとに最良近似式を求める計算を2回行なった結果のグラフです。
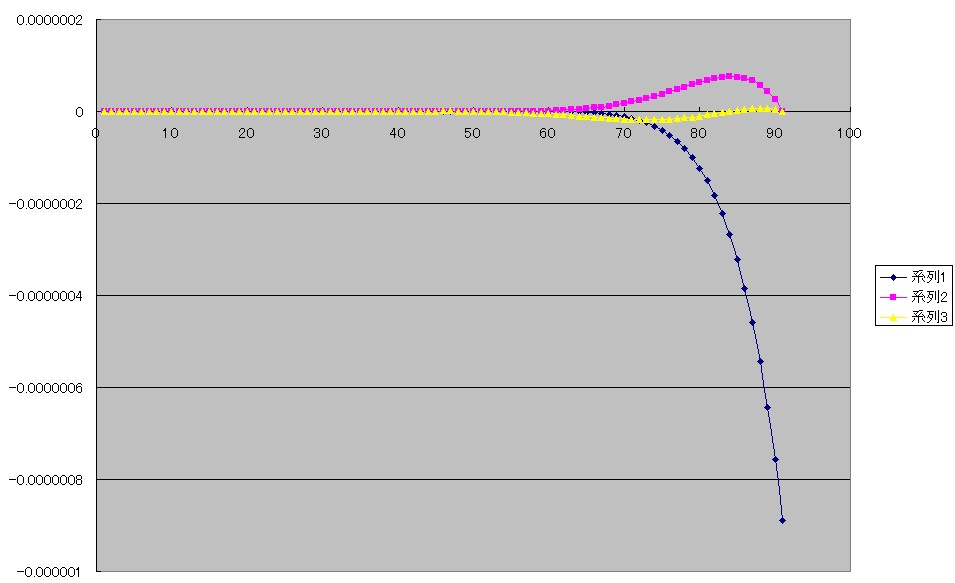
今までと同様、E(x)=f(x)−g(x)のグラフです。
系列1がチェビシェフの近似式で、系列2、系列3が1回目、2回目の計算の結果求められた近似式です。
当初の予想に反して、1回目の計算(系列2)から、割と良い形のグラフになっています。
しかし上のグラフでは、全体としては予想外に良い形であることはわかりましたが、系列1のために縦方向が圧縮されてしまって、途中の振幅がほとんど確認できません。
そこで系列1の表示を途中までで止めてみました。
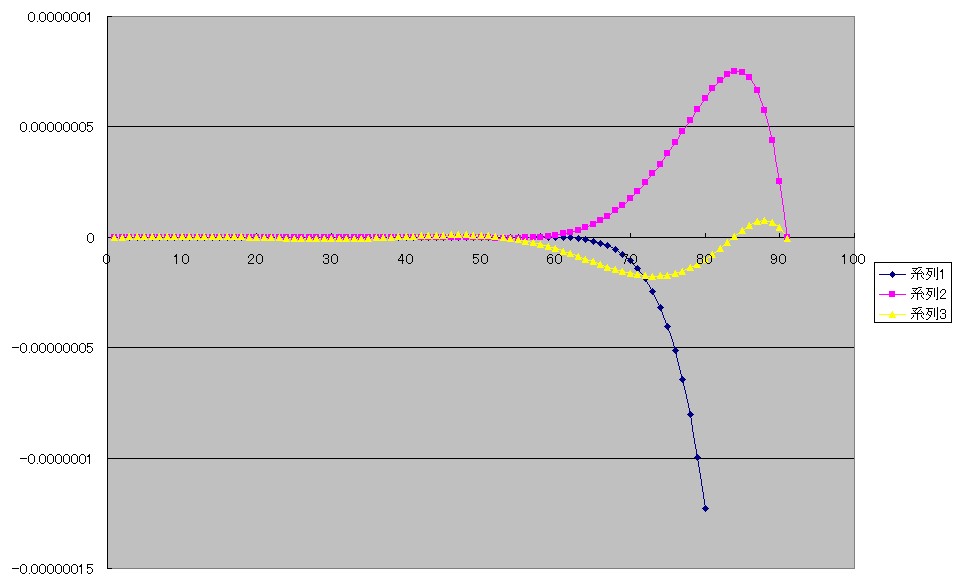
うーん。
これでもまだ途中の形はわかりませんねえ。
思い切って表示を55°あたりまでで止めてみました。
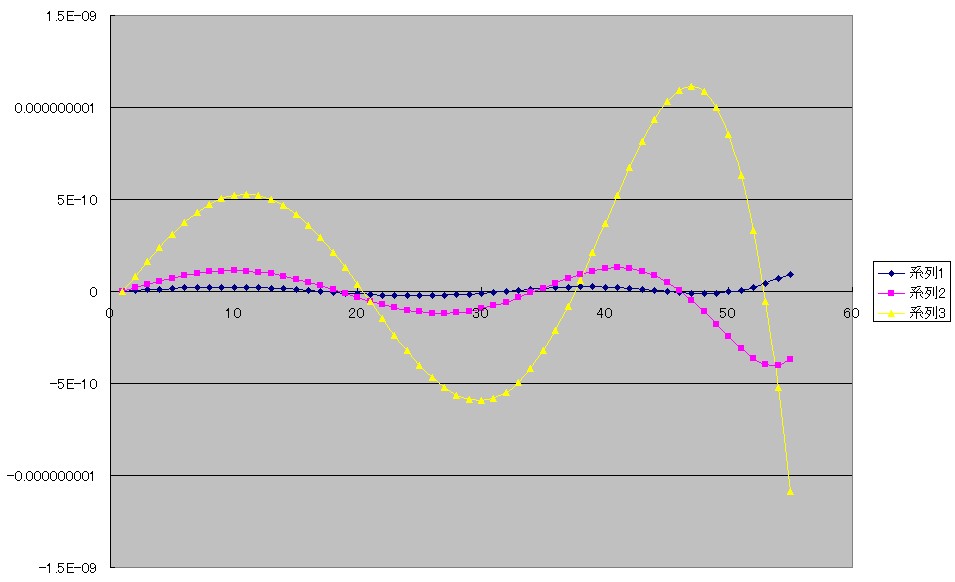
おお、ちゃんとしっかりした形になっています。
これなら最後まで計算できそうです。
ということで、続けて計算をしてみました。
下がそのグラフです。
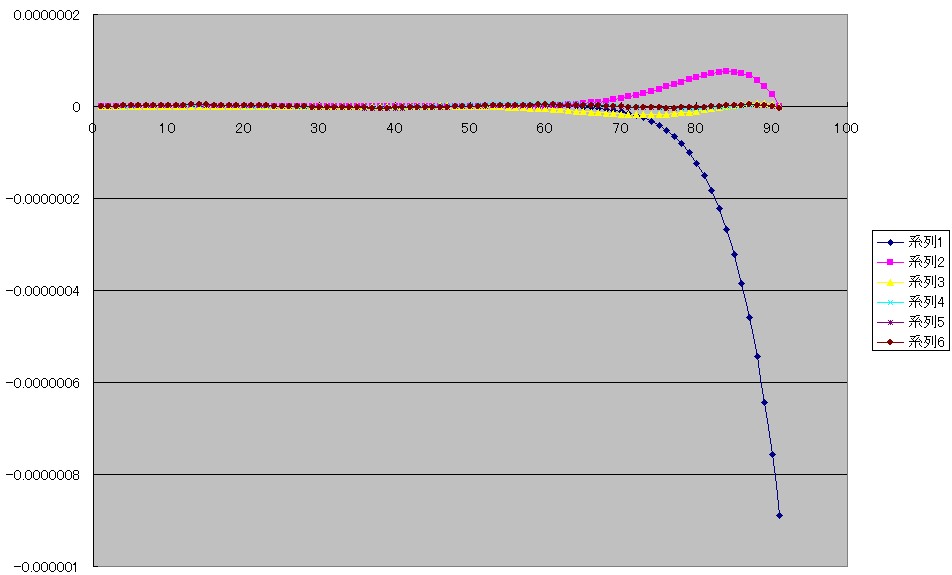
やっぱり系列1、系列2の誤差が大きいため、その後の計算の結果がよく見えませんが、系列6が最終結果になりました。
下は系列1から系列3までの表示を途中までにしたときの、結果のグラフです。
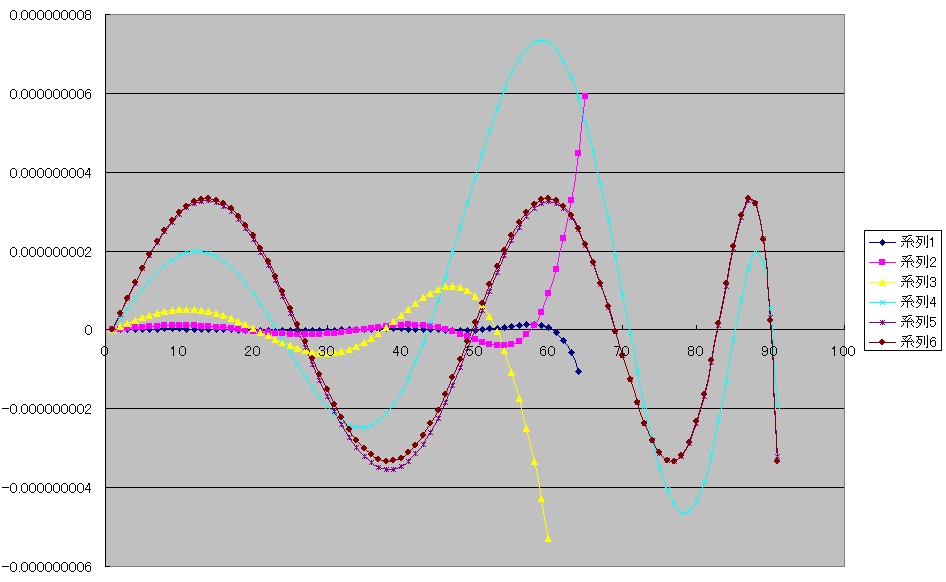
系列6は前回求めた系列9のグラフと全く同じ式になりました。
今回の結果から、範囲を少しずつ拡大しながら最良近似式を求める計算を行なっても、また最初から全範囲を対象にして計算を行なっても、求まる最良近似式は同じであることがわかりました。
しかも最初から全範囲を対象として計算したほうが3回分も少ない計算回数で最終結果に到達できることがわかりました。
MYCPU80でCP/Mを![第60回]
2014.11.1upload
前へ
次へ
ホームページトップへ戻る