超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第59回]
●最良近似式に至る途中のグラフ
前回はなぜ最良近似式が必要なのか、というその理由について書きました。
それがご理解いただけたところで、いよいよ最良近似式の算出方法についての説明にかかります。
が。
実はその方法につきましては、「数値計算」(赤坂隆著。コロナ社刊)に説明があるのですが、何回読んでもなかなかその意味が理解できませんでした。
こうすれば求まる、ということで数式と文章だけで説明してあるものですから、それがどういうことなのか、具体的なイメージが捉えられなくて理解が及ばなかったのです。
そこで実際の計算手法の説明に入る前に、具体的なイメージをまずつかんでいただくために、計算過程のグラフを見ていただくことにいたします。
最良近似式は元になる近似式(通常はチェビシェフの近似式)を補正しつつより最良な近似式へと近づけていくという計算手法で求めます(他にも方法があるのかもしれませんが、私がやっと理解できたのはその手法のみです)。
下はチェビシェフの近似式からスタートして最良近似式に至るまでの途中の過程のグラフをプロットしたものです。
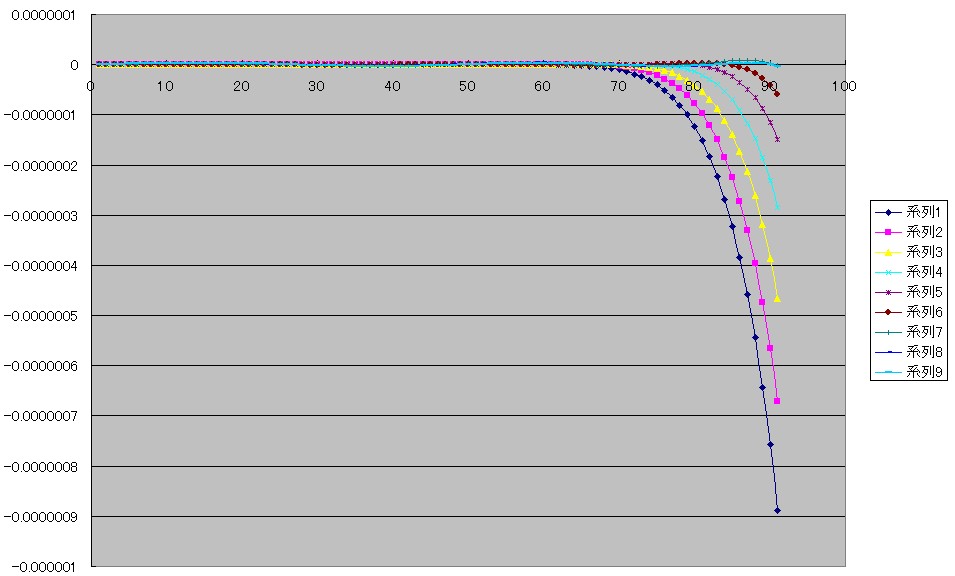
いずれもE(x)=f(x)−g(x)のグラフです。
系列1は前回も見ていただいたチェビシェフの多項式です。
系列9は[第57回]で見ていただいた、私が算出した最良近似式です。
[第57回]のグラフと全然違うじゃないか、と思われるかも知れませんが、縦のスケールが全然違うのです。
[第57回]のグラフは最良近似式のみでしたので縦の目盛り(E(x)の値)は0.2×10−8きざみなのに対し、今回のグラフはチェビシェフの多項式の誤差が大きいためにそれが影響して縦の目盛りが0.1×10−6と縦が50分の1に圧縮されてしまっています。
そのため上のグラフでは系列9(最良近似式)は0の線上にはりついてしまっているようにしか見えません。
ですけれど、上のグラフを見ていただきますと、系列2から系列8へと、最初は大きかった90°近辺の誤差の値が少しずつ小さくなっていくのが理解できると思います。
下のグラフは前回見ていただいたものです。
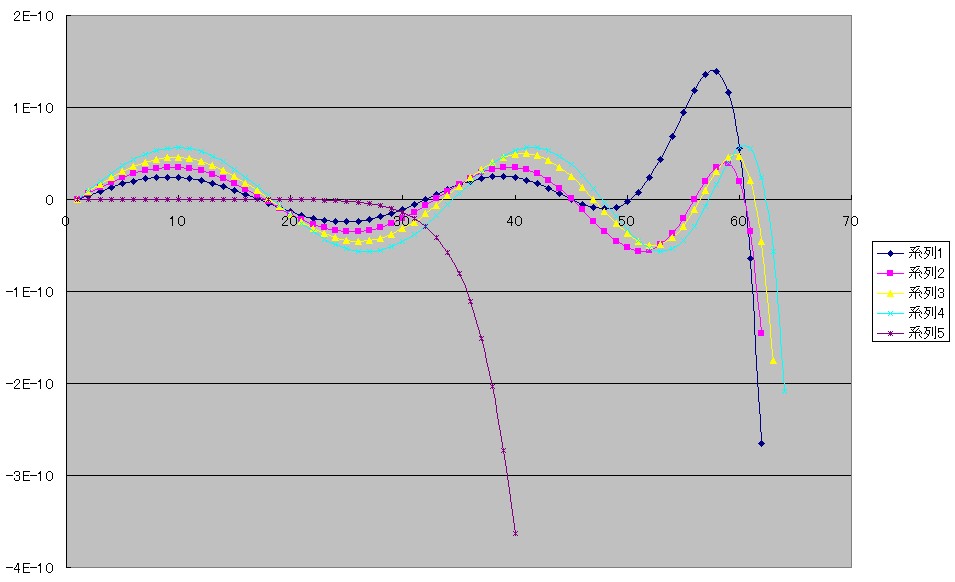
系列1がチェビシェフの近似式の誤差のグラフです。
系列2から系列4はそれを少しずつ補正していく過程の式の誤差のグラフです。
チェビシェフの近似式が60°くらいまではほぼ最良近似式の形に近いことに注目して最初は計算の範囲を0°から60°までにしてスタートし、それから1°きざみに範囲を拡大しながら計算をおこなっています。
それがうまくいったように思えましたので、刻み値を2°に広げて再計算してみたのが下のグラフです。
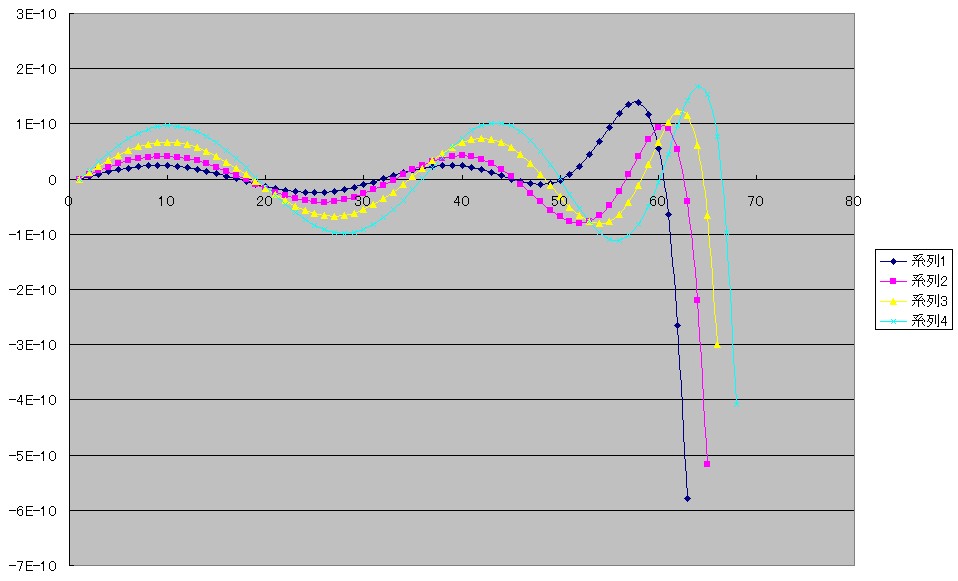
計算は60°を少し越えるところまでの範囲で行なっていますが、そこで求めた式がそれより大きな角度で使えないということではありません。
今回の最初に見ていただいたグラフでわかりますように90°まで代入でき、かつそのときの誤差の値も少しずつ小さくなってきています。
ただ途中の過程の式での90°までの全範囲の誤差を上のグラフにプロットすると、最初に見ていただいたグラフのように縦方向が圧縮されてしまいます。
そこで途中の過程の式における誤差の値は縦方向のグラフの範囲を超えない値まででグラフにプロットするのを打ち切っています。
今回の計算結果のグラフでは、1°きざみのときに比べてちょっと振幅が大きくなったような気がしますが、それでも形は悪くないように思いましたので、今度は思い切って5°きざみにして再計算してみたのが下のグラフです。
60°から2°きざみで計算すると、範囲を90°までに広げるためには15回ほども計算しなければならない、というのがそのようにした理由です。
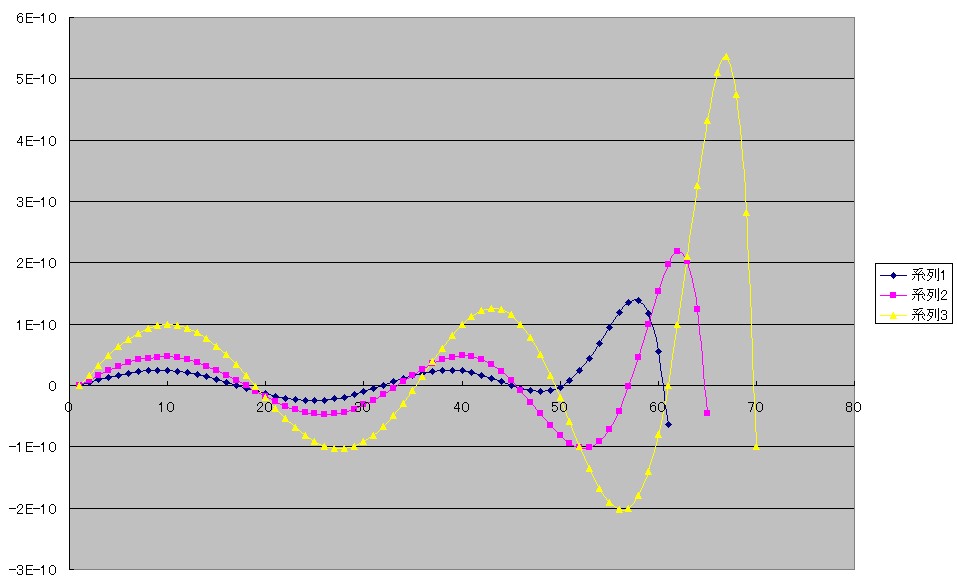
なんだかやばそうな形になってしまいました。
このような形になるのには理由があって、それについてはのちほど具体的な計算のところで説明しますが、刻み値を大きく取ることで、計算のもとになる誤差の値も大きくなるために、大きな値の近くでは一度では補正できなくてどうしても振幅が大きくなってしまいます。
小さな刻み値で細かく計算していったときと、荒く計算したときとで得られる結果が異なるのかどうかについてはまだ検証していません。
とりあえずその点については気にしないでそのまま計算を続けていった結果を全てプロットしたのが下のグラフです。
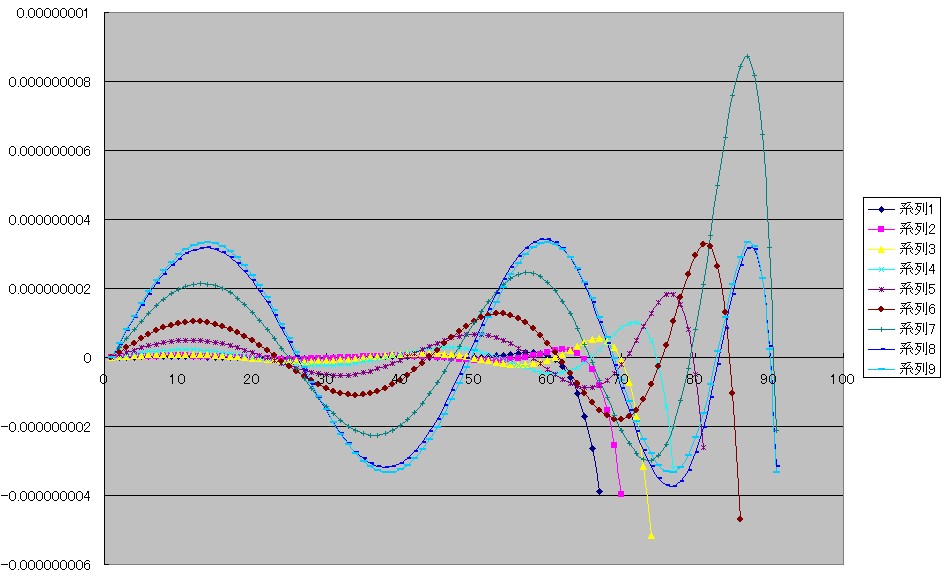
系列9が[第57回]で見ていただいたのと同じ、最終的に求められた最良近似式です。
ここでも系列7の振幅が急に大きくなっているのがちょっと気になりますが、それでも次の系列8で落ち着いたので、まあいいか、ということにいたしました。
うーん。
ちょっと気になりますねえ。
計算ミスをしていないかどうか、調べてみることにいたしましょう。
MYCPU80でCP/Mを![第59回]
2014.10.30upload
前へ
次へ
ホームページトップへ戻る