超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第57回]
●ついに!最良近似式!
前回は考察の途中で時間切れとなってしまいました。
そのまま、また何日か間が空いてしまいました。
ご注文が重なってしまって、ホームページの更新にまで手が回らなかったということもありましたが、最良近似式について今ひとつ納得できなくて、不得要領なまま書くのがどうにも気が進まなかったということでもありました。
しかし、しかし!
とうとう、やりました!
最良近似式の求め方がどうにも理解できなくてこのところずっと悩んでおりました。
それがとうとう、突然に「わかったぞお!」という瞬間がやってきました。
ええ、もうすっかりわかってしまいました。
もう何回も書いていることなのですけれど、とにかく何回読んでも、考えてもさっぱりわからない、そこから先にどうしても進めない、といったふうな状況に陥っても決して諦めてはいけません。
そこで諦めないでもう一歩進んでみようということでがんばっておりますと、突然、本当に突然、ぱっと霧が晴れて一気に視界が開けてしまう瞬間が必ずやってきます。
こうなると、もう宗教ですな。
何はともあれ、まずはその成果をお目にかけましょう。
最良近似式のグラフです。
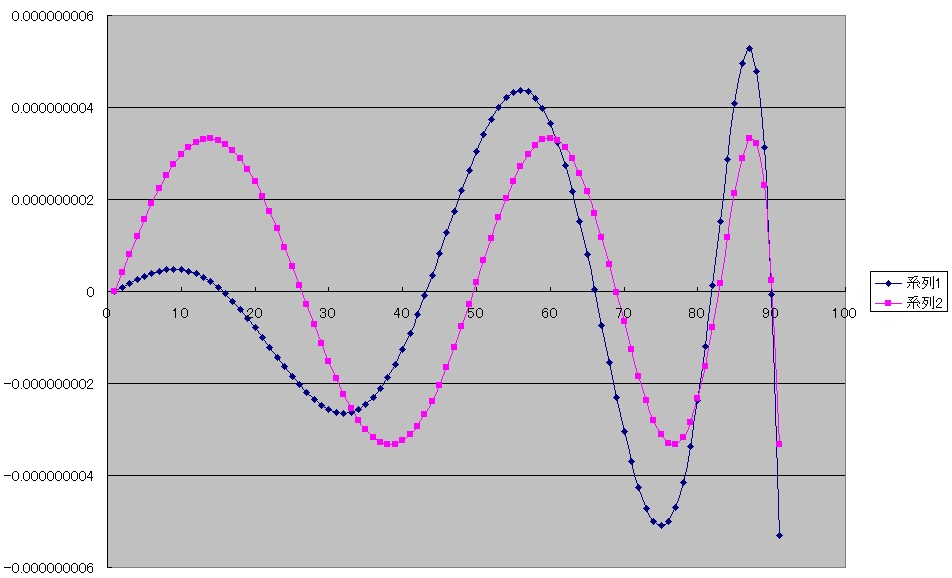
系列1(紺色)は「数値計算」(赤坂隆著。コロナ社刊)110ページの表から引用してEXCEL上にプロットしたsin(x)の最良近似式(下の式)の誤差のグラフです。
(横軸は範囲0°〜90°、1°きざみ)
sin(πx/2)=c1x+c3x3+…+c9x9
c1=1.57079631847
c3=−0.64596371106
c5=0.07968967928
c7=−0.00467376557
c9=0.00015148419
そしてご注目いただきたいのが系列2のグラフ(ピンク色)です。
ついさきほど私が計算で求めた最良近似式(下の式)の誤差のグラフです。
sin(x)=c1x+c3x3+…+c9x9
c1=0.999999977
c3=−0.166666477
c5=0.0083329
c7=−0.000198009
c9=2.59054×10−6
「数値計算」の式は変数がπx/2になっていますが、私の求めた式は変数がxなので係数は異なりますが求めているものは同じです(単位はラジアン)。
ある関数の式をf(x)、その最良近似式をg(x)とするとき、両式の差(つまり誤差)
E(x)=y(x)−g(x)
のグラフは正負交互に極値β、−βを取りながら振動する、と定義されています。
そこで上のグラフを見ますと、系列1は角度が大きい範囲で振幅が大きくなっています。
しかし私が求めた系列2はほとんど同じ振幅で、かつ誤差の最大値は系列1よりも小さくなっています。
えっと。ちょっと面映いのですが。
私の求めた式のほうが、より「最良近似式」かと。
ま。実情を考えますと、さほど自慢になるほどのことでもありませんが。
「数値計算」の表は他の文献からの引用となっています。
同書巻末の引用元のリストによりますと、引用元は
C.Hastings,Jr.:Approximations for Digital Computers,Princeton Univ.Press(1955)
となっています。
60年前ですものね。
どうやって計算したのでしょう?
おそらく当時はこれが計算の限界だったのでありましょう。
あ。
算出方法につきましても順を追って説明いたしますが、なにしろ大変な計算なのです。
ええ。
なんたってご覧の通りの長い桁の数の6元1次連立方程式を繰り返し解いていくという恐ろしい計算をしなければなりません。
(勢い、説明も大変なところに入っていってしまいます)
次回に続きます。
MYCPU80でCP/Mを![第57回]
2014.10.28upload
前へ
次へ
ホームページトップへ戻る