超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第56回]
●最良近似式について
このところ関数の近似式について考察を続けてきました。
当テーマとしましては、またまた相当に脱線してしまっております。
いい加減に本題に復帰しなければならないのですけれど、なかなか思うに任せません。
ただ最近になりまして、やっと一応の理解に達したように思います。
関数の近似式につきましては、テイラーの多項式しか知らなかったことから比べれば大いなる進歩です。
あ。
全くの道草というわけでもありませんで、BASICの三角関数などについては、今までよそ様のお作りになった近似式をそのままいただいておりましたので、そこのところをなんとか自前で開発してみたいものだという気持ちもあってのことです。
ようやくチェビシェフの近似式にまで理解が及ぶことになりました。
ところが、再々引用しております「数値計算」(赤坂隆著。コロナ社)によりますと、チェビシェフの「近似式」は厳密には近似式ではなく、最良近似式を導き出すための第一近似式に過ぎないのだそうです。
なるほどチェビシェフの近似式と「数値計算」所載の最良近似式のそれぞれの誤差のグラフを比べてみますと、その差は一目瞭然です([第48回]参照)。
私は近似式なるものは、ただ一様に誤差が少ないものと思っていましたが、そういうものではないようです。
テイラーの多項式は次数を高めていきますと、xが小さい範囲ではどんどん真の値に近づいていきます。
しかしxの値が大きくなっていくにつれて誤差が急激に増大します。
ところが最良近似式では誤差はある一定限度で増減を繰り返します。
それはxが大きくなっても変わらないようです。
そこのところがチェビシェフの近似式と最良近似式との大きな違いです。
チェビシェフの近似式も誤差は一定の限度で増減しますが、xが大きくなっていく途中のある点から誤差が急増します。
テイラーの多項式もxの小さい範囲で見れば誤差は増減を繰り返しますが、チェビシェフの近似式よりも小さいxの値から誤差が急増します。
さてそういうことになりますと、ぜひともその最良近似式なるものをわがものにしたいと思うのが人情でありまして、先日から時間をみつけてはその理解に努めてきました。
最良近似式の求め方につきましては「数値計算」にその説明があるのですが、これが実に難解で(そう思うのは己の頭の悪さゆえでありましょうけれど)、さっぱりちんぷんかんぷんで何がなんだかわけわかめ状態でありました。
が。
読書百遍、意おのずから通ず、のたとえにもあります通り、いえ、とても百遍もは読んではおりませんが、わからないながらも繰り返し繰り返し読んでおりますと、突然に霧が晴れて、なんだか「わかったぞお」という境地に至ったように思います。
しかし。
理解はできた、ようには思うのでありますが、とんでもないことまで、わかってしまったようであります。
最良近似式を求める過程では多元連立方程式を解かねばならないのですが、その変数たるや、係数値を真の値に近づけるための微小な補正値を仮定しているために、大きな数値の減算を繰り返すと桁落ちの誤差によって、何を求めているのかわからなくなってしまう、というとんでもないあぶないしろものでありました。
おそらくたかだか数桁の有効数字の近似式を求めるためにも、おそらく倍精度以上の演算が必要でありましょう。
さらに、そもそも最良近似式を求めるための「仮定」が私には難題のように思えます。
ま、しかし、パズルは難しいから面白いのと同じでありまして、難題大いに結構、いずれ見事に解いてみせましょうぞ、と思ってはおりますが、これ以上ここにこだわっておりますと、肝心のMYCPU80用CP/M互換DOSがいつになってもできあがりませぬ。
最良近似式につきましては不本意ながら、このあたりで一旦棚上げにしておきたいと思います。
それにつきましては、いずれまたトライするときのために、これまでに理解したと思うことを、備忘録として以下整理しておきたいと思います。
自分では理解したつもりでおりますが、間違っていることもあるかもしれません。
もし間違いにお気付きになられましたら、メールにてご指摘いただきますようお願いいたします。
以下、最良近似式の求め方です。
今求める関数f(x)の近似関数y(x)があって、
E(x)=f(x)−y(x) …(1)
としたときに、E(x)のグラフが0をはさんで+−に一定の範囲で振動するような形になるとき、y(x)がf(x)の最良近似であるといえます。
ここにE(x)はf(x)に対するy(x)の誤差の関数です。
下のグラフは[第48回]のSIN(x)に対するチェビシェフの9次の近似式の誤差のグラフを絶対値ではなく正負の値でプロットしたものです。
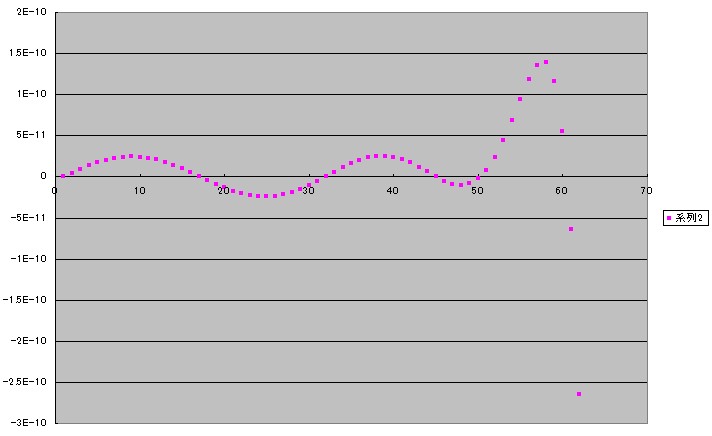
横軸はx(単位は角度 °)。
xが大きくなると誤差が急増するためグラフは途中までの値で打ち切っています。
このグラフで見ると大体45°近くまでは誤差が一定の範囲で振動していますが、50°を越えるあたりから急に増大し一旦正の最大値をつけたあと、マイナスに向かって急降下しています。
この途中までのグラフの形が最良近似の形だといえます。
以下説明を簡単にするため、「数値計算」での説明にしたがって、2次式について考えることにします。
いま上記、式(1)の近似式としてチェビシェフの2次の近似式
y(x)=c0+c1x+c2x2 …(2)
を得たとします。
これはまだ最良近似式ではありませんが、それに近い近似式です。
y(x)は2次式で、上のE(x)も2次式で考えますから、2点x1、x2で2つの極値β1、−β2を持ちます。
x1、x2を偏差点といいます。
上のグラフは9次式ですが、xの偶数次の項がなく、x,x3,x5,x7,x9の実質5次式なので、5個の極値があります。
区間の両端も極値に数えますがここでは除外して考えます。
ここでE(x)の式はx1、x2を代入すると
f(x1)−(c0+c1x1+c2x12)=β1 …(3)
f(x2)−(c0+c1x2+c2x22)=−β2 …(4)
と書けます。
ところで求める最良近似式を
g(x)=d0+d1x+d2x2 …(5)
としたときg(x)でもy(x)と同じように書けますが、そのときの偏差点は厳密にはx1、x2とは異なります。
しかしそのままではその先計算ができませんから上のy(x)のときのx1、x2を仮に当てはめて、
f(x1)−(d0+d1x1+d2x12)=β …(6)
f(x2)−(d0+d1x2+d2x22)=−β …(7)
とします。
最良近似式では正負誤差の最大値は絶対値が等しい値になります(と仮定します)から、上の式の右辺はβおよび−βになります。
またx1、x2では上の式のグラフは傾きが0になりますから、上式を微分して
f’(x1)−(d1+2d2x1)=0 …(8)
f’(x2)−(d1+2d2x2)=0 …(9)
と書けます。
説明の途中ですが本日は時間がなくなってしまいました。
この続きは次回にいたします。
MYCPU80でCP/Mを![第56回]
2014.10.23upload
前へ
次へ
ホームページトップへ戻る