超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第48回]
●sin(x)の近似式の誤差のグラフ
今回は[第46回]で求めましたsin(x)の3次までのチェビシェフの近似式をテイラーの多項式と比較してみました。
下のグラフはEXCELで計算した0°〜90°までのsin(x)の値とチェビシェフの近似式sin(x)=−(5/32)x3+(383/384)xとの差の絶対値をプロットしたものです(ピンク)。
比較のために、同じくEXCELで計算したsin(x)とテイラーの5次の多項式sin(x)=x−(1/3!)x3+(1/5!)x5 との差の絶対値を青色で、また同じくEXCELで計算したsin(x)とsin(x)=x−(1/3!)x3との差の絶対値を黄色でプロットしました。
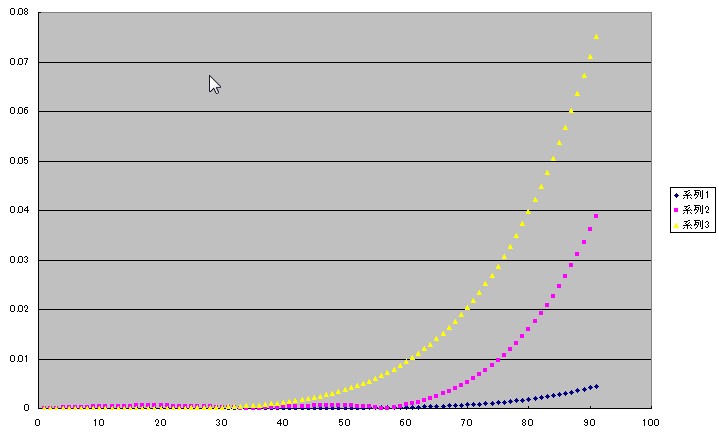
グラフで見ますとチェビシェフの近似式(3次式)はテイラーの多項式の5次式と3次式の間にあることがわかります。
むむ。
確かになかなかに見事なものです。
しかもテイラーの3次式はさすがに無理がありますから、40°を越えるあたりから誤差が急に増大していますが、チェビシェフの近似式は同じ3次式でありながら60°近くまでテイラーの5次式に近い小さな誤差でがんばっています。
おおそういえば60°といえばおよそラジアン1に相当します。
ということで0°から60°までに範囲をしぼって同じようにグラフ化してみました。
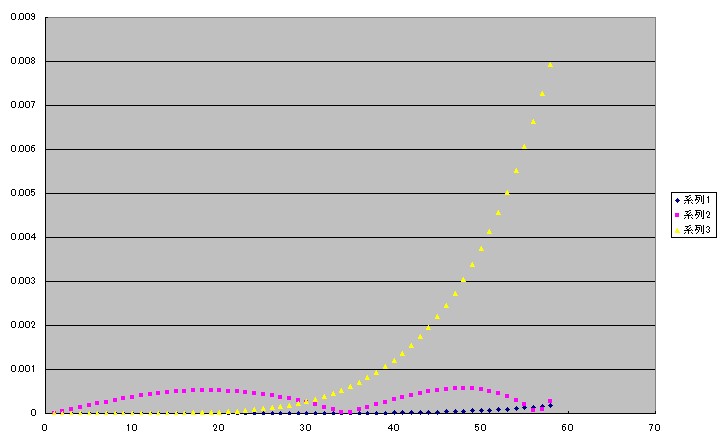
この範囲でもテイラーの3次式は約30°あたりから誤差が急に大きくなっています。
さすがに5次式は0°から60°の全範囲で小さな誤差に収まっています。
チェビシェフの3次式はその範囲では5次式よりも大きい誤差で、かつ30°近くまではテイラーの3次式よりも誤差が大きいのですが、しかし0°〜60°の全範囲でおおよそ平均的な誤差になっているように見えます。
これを見ますと、チェビシェフの近似式はやはり只者ではなさそうです。
3次式や5次式では本当のところはよくわからないように思いまして、EXCELでもっと高次の式まで計算で求めてみました。
それも同じようにしてグラフにプロットしました。
チェビシェフの9次式(ピンク)とテイラーの11次式(青色)と同じくテイラーの9次式(黄色)です。
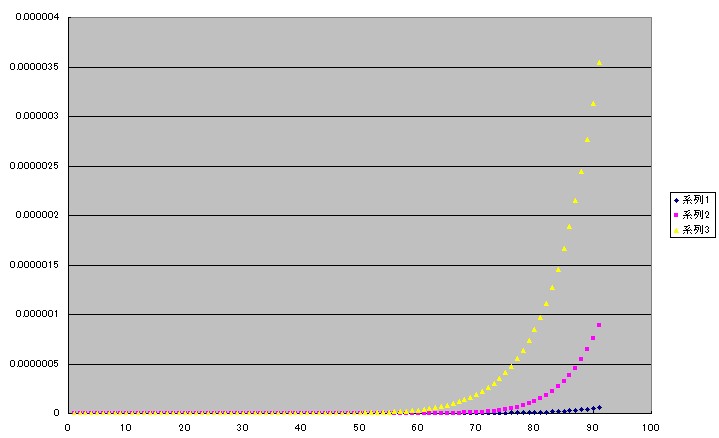
3次式の場合とよく似ていますが、チェビシェフの近似式の誤差が75°近くまで小さいままで収まっているように見えます。
範囲を60°までにしてグラフにプロットしてみました。
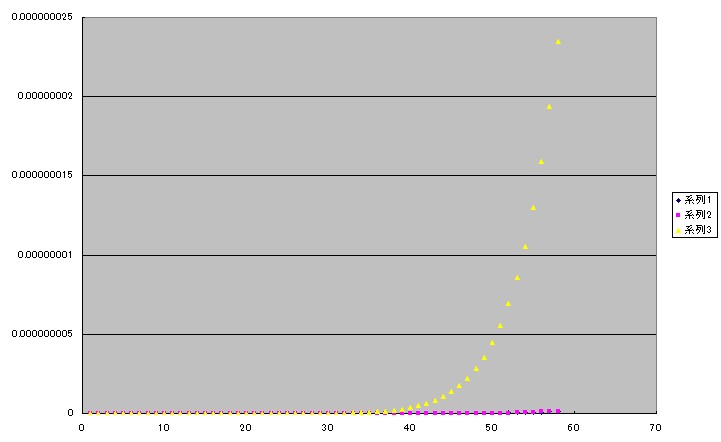
チェビシェフの9次式の誤差はテイラーの11次式の誤差に重なってしまっているように見えます。
縦軸をもっと大きくできるようにテイラーの9次式は外してみました。
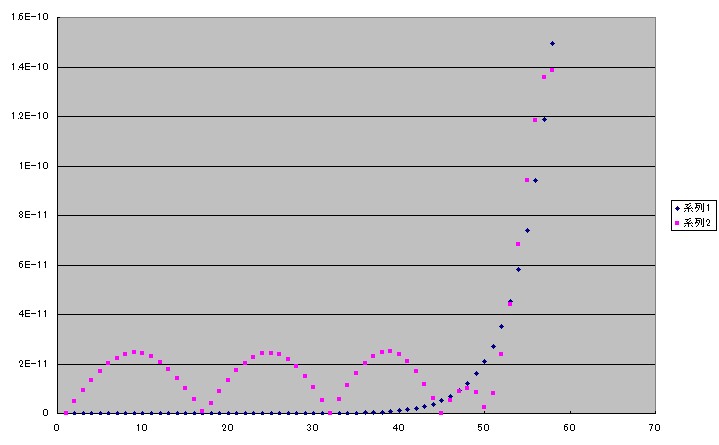
おお。
なんだかちょっとすごい感じです。
チェビシェフの近似式のほうはなんとか誤差を少なくしようとがんばっているように見えます。
しかしこのグラフを見る限りではチェビシェフの9次の近似式はテイラーの11次式にはとてもかなわないように見えます。
それでは果たして「最良近似式」なるものの実力はいかほどでありましょうか?
コロナ社「数値計算」に記載されております9次の最良近似式(ピンク)をテイラーの11次の多項式(青色)と比較してみました。
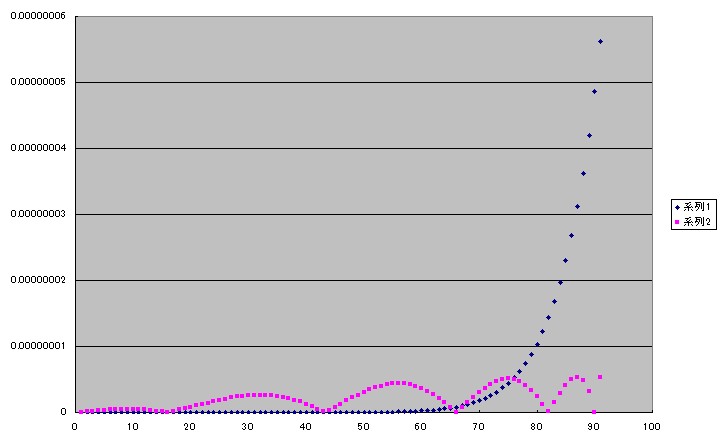
おお。
これは!
なんと、「目からうろこ」の感があります。
これが最良近似式か!
むむ。
まさに、「最良」でありましょう。
MYCPU80でCP/Mを![第48回]
2014.10.7upload
前へ
次へ
ホームページトップへ戻る