超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第49回]
●EXCELでチェビシェフの近似式を求める
前回はEXCELでsin(x)を計算し、その値とテイラーの多項式、チェビシェフの近似式での計算結果とのそれぞれの差をグラフにプロットしてみました。
こういうときにEXCELはなかなかに便利です。
チェビシェフの近似式の求め方は[第46回]で説明しました。
そこでは例としてテイラーの5次式から3次の近似式を求めました。
3次式ですからなんとか手計算でも求めることができたのですが、9次式となるととても手計算では求められません。
電卓を使えばできないことはないでしょうけれど、そりゃあ大変です。
昔はそれでもそうするより仕方がなかったのでしょうけれど、今は有難いことにEXCELを使えば簡単に求めることができます。
ちなみにチェビシェフの9次の近似式を求めるためにはテイラーの11次の多項式をもとに計算します。
もうその時点でかなり大変です。
テイラーの11次の多項式を降順にして示しますとこうなります。
sin(x)=−x11/11!+x9/9!−x7/7!+x5/5!−x3/3!+x
=−x11/39916800+x9/362880−x7/5040+x5/120−x3/6+x
1/39916800なんて計算をしなければならないのですから、EXCELの有難さがわかろうというものです。
[第46回]で説明しました方法は、テイラーの多項式と同じ次数のチェビシェフの多項式を使って、連立方程式の消去法と同じ算法で高次のものから順にその次数の項を消去できるような係数を求めていきます。
そのようにして順次求めた係数を最高次のみ無視して、その下の次数のTn(x)にそれぞれ乗じてxの多項式を求めると、それがチェビシェフの近似式になります。
[第46回]で説明しましたのはそういうことなのですが、ご理解できましたでしょうか。
それをEXCELでやりましたのが下の画像です。
この方法はEXCELを使ってもちょいと面倒です。
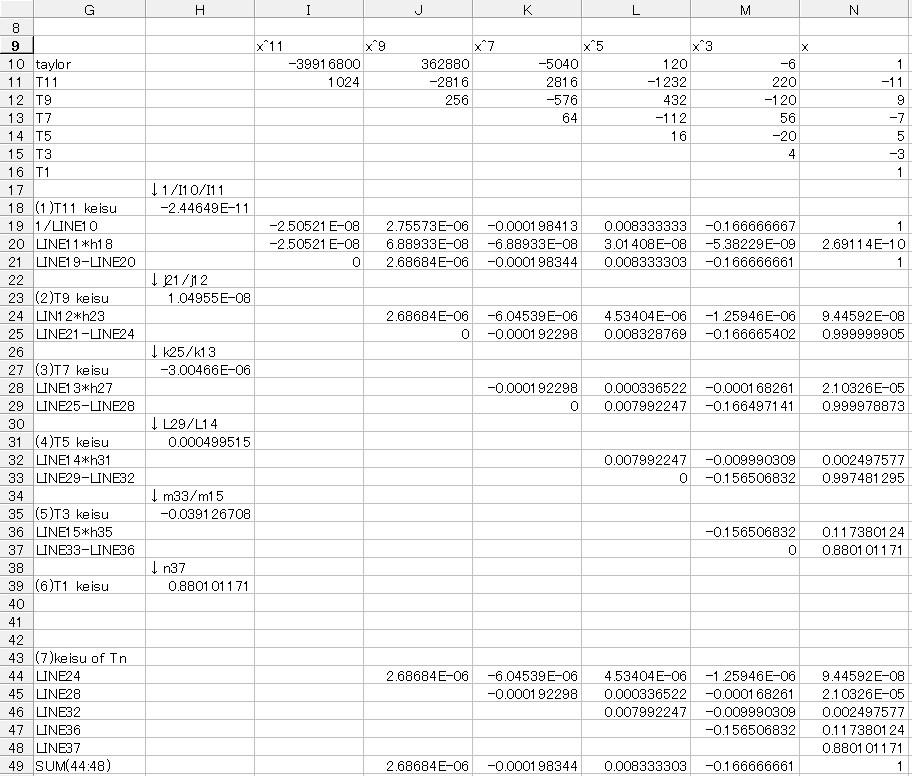
LINE10にテイラーの多項式のXnの係数を記入します。
ここの値は本当は1/n!なのですがいきなりそれを記入すると全部小数になってしまいます。
あとから見るとなんだこの数字は?ということになりかねませんから、ここは分母の数を書きました。
実はM10には =−2*3 が埋めてあります。
L10には =−M10*4*5 が埋めてあります。
K10には =−L10*6*7 が、J10には =−K10*8*9が、I10には =−J10*10*11が埋めてあります。
EXCELは便利ですね。
LINE11からLINE16には[第45回]で算出しましたチェビシェフの多項式のT11、T9、T7、T5、T3、TのXの係数をそれぞれ書き込みます。
まず最初にX11の項を消去するためT11の係数を求めます。
H18には =1/I10/I11 が埋めてあります。
LINE19はテイラーの11次式の各係数が置かれています。LINE10の逆数です。
LINE20にはLINE11×H18を計算した結果を格納します。
LINE19−LINE20を計算するとX11の項が消去されます。
このとき求めたH18の値がT11の係数ですが、これは最終段階では無視することになります。
必要なのはその次以下で求めるT9〜T1の係数です。
上の計算でX11の項を消去して求められたLINE21の値をもとにして同じ考え方で今度はX9の項を消去します。
H23の値が求めるT9の係数になります。
以下順にTnの各係数を求めていきます。
実はそのような計算の過程で、Xnの項を消去するために求めたTnの係数をTnの行に乗じたものがそのまま求める近似式の一部になっていますから、それをそのままLINE44からLINE48に転記したうえで最後に各列を合計しています。
LINE49がチェビシェフの9次の近似式の各係数です。
下はLINE49を普通の数式の形で示したものです。
sin(x)=2.68684E−6*x9−0.000198344x7+0.008333303x5−0.166666661x3+x
MYCPU80でCP/Mを![第49回]
2014.10.8upload
前へ
次へ
ホームページトップへ戻る