超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第63回]
●連立方程式の解法
今朝になりましてから前回の記事を読みましたら、説明が間違っていることに気が付きました。
その説明のままでは方程式が解けません。
そこでちゃんと式が解けるように、説明を書き直しました。
本日早朝までにご訪問いただきました方はひょっとして訂正前の記事をお読みいただいたかも知れません。
誠に申し訳ありませんが、前回をご再読いただきますようお願い申し上げます。
さてその前回は、最良近似式を求めるためには連立方程式を解く必要がある、というところまで説明をいたしました。
今回はその連立方程式の解き方について説明いたします。
連立方程式は中学校で習いました。
代入法だとか消去法だとかという方法を習いました。
最良近似式を求めるための連立方程式も中学で習った方法で解けないことはありませんが、そりゃあ大変です。
中学の頃の試験問題はたいてい答えは切のいい1〜2桁の整数になると決っていました。
しかし世の中の現実はそんな甘いものではありません。
前回も終わりのところで少し書きましたように、小数点以下6〜7桁もあるような数値の多元連立方程式を繰り返し何回も解かなければなりません。
とてもとても習ったような方法では解けるものではありません。
ここではその解法として行列による方法を考えます。
例として次の連立方程式を考えます。
この式は「数値計算」(赤坂隆著。コロナ社刊)にあった例題です。
2x+3y+4z=6
3x+5y+2z=5
4x+3y+30z=32
この例題は行列なんて考えなくても中学で習った方法のほうが簡単に解けてしまいそうです。
その昔、大学に入ったばかりのころ、私は不真面目な学生で、講義をさぼって遊んでばかりおりました。
やがて期末試験になり、さすがにこればかりはさぼるわけにはいきませんので、ぶっつけ本番で試験に臨みましたところ、上と同じような問題が出されておりました。
なにしろ講義には全く出席しないで遊んでおりましたから、まともに問題が解けるわけが無い、仕方がないのでダルマの絵でも描いて出そう(手も足も出ませんの意)ぐらいの気持ちでおりましたので、
「何だ、この問題は」
かえって拍子抜けがしてしまいました。
そこで堂々と中学で習った通りの方法で解いて、答案を提出いたしました。
さすがに「優」ではなかったと思いますが、かろうじてお涙の「可」をいただいたように思います。
思えば出来の悪い学生でありました。
もっと勉強をしておくべきでありました。
この歳になりまして、誠に慙愧に耐えません。
本題に戻ります。
上記の式を行列を用いて表すと下のようになります。
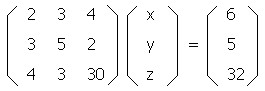
これは式の表現を変えただけですから、まだ答えはでません。
そこで、ここからがマジックなのですが。
いまここで
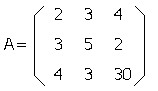
と書くことにします。
そしてAの逆行列A−1を用いて
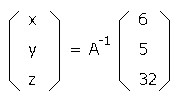
という式を考えます。
これを計算することでx,y,zの値を得ることができます(だそうです)。
なんじゃあ、こりゃあ。
まるで手品ではないか。
むむ。
本当にちゃんと求まりますかいな。
ちょいと心配ではありますが、このまま次回に続きます。
MYCPU80でCP/Mを![第63回]
2014.11.6upload
前へ
次へ
ホームページトップへ戻る