超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第64回]
●逆行列
前回は下記の連立方程式の解法について書きました。
まずはそのおさらいです。
例として下の連立方程式を考えます。
2x+3y+4z=6
3x+5y+2z=5
4x+3y+30z=32
上記の式を行列を用いて表します。
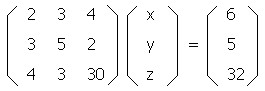
ここで
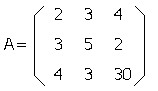
と書くことにします。
そしてAの逆行列A−1を用いて
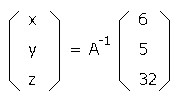
という式を考えます。
これを計算するとx,y,zの値が求まります。
というところまで説明をしました。
すると次は当然逆行列A−1について説明をしなければなりません。
逆行列A−1は下の式で表されます。

adjAはAの余因子行列(adjugate matrix)で|A|はAの行列式です。
さあ、わからなくなってきました。
もうさっぱりわけわかめ状態です。
でもここを通過すれば何か魔法の力によって連立方程式が簡単に解けるようになるのかも(ほんとうか?)。
そこでまずは余因子行列について説明をいたします。
●余因子行列
ところがこれがまたなかなかに理解するのが厄介な代物なのです。
とにかくややこしい。
まずは余因子の行列というのを考えます。
「余因子行列」ではありません。
「余因子」の「行列」です。
Aを

としたときの、Aの余因子の行列です。
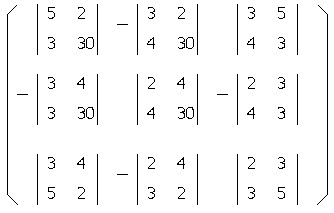
行列の各要素に注目して、その要素の行と列を除外した残りの要素の行列式に、その位置によって負号をつけたものが余因子です。
負号は奇数行かつ偶数列か偶数行かつ奇数列につけられます。
たとえば左上の「2」の余因子は、「2」の行と列を除外するとその斜め下の5、2、3、30が残りますからその並びのまま行列式にしたものです。
●行列と行列式
もうどんどんややこしくなってきます。
行列は一塊の数値を一定の並び順に配置して()で囲ったもので、並び方には意味がありますが、固有の値というものはありません。
それに対して行列式は各要素を行列と同じように並べて| |で囲います。
行列式は各要素間に固有の計算式が適用され、その結果固有の値を持つます。
下の左辺の行列式の値は右辺の計算の結果となります。
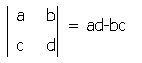
ですから上の余因子の行列で示されている行列式は
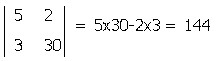
のように計算されます。
全部の行列式を計算すると、結局Aの余因子の行列は下のように表されます。

ここでそのようにして求められた余因子の行列の行と列を入れ替えます。
行列の行と列を入れ替えたものをもとの行列の転置行列といいます。
それが余因子行列 adj A です。
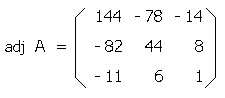
やれやれ。
これでやっと余因子行列 adj A が求まりました。
次は行列式 |A| です。
●行列式 |A|
Aの行列式は下のように表され、それを計算するとその値は−2になります。

行列式の値については先程2×2の行列式について説明しましたが、3×3の行列式でも同じように計算します。
各要素を右斜めに掛けたものから左斜めに掛けたものを引きます。
2X5X30+3X2X4+4X3X3−2X2X3−3X3X30−4X5X4=300+24+36−12−270−80=−2
それとは別の計算もできます。
実は上の計算は、さきほどの余因子の行列を求めたときの一番上の行の要素と余因子との掛け算と同じになります。
たとえば2X5X30−2X2X3は2X(5X30−2X3)と同じです。
そこで下のように計算することができます。
2X144+3X(−82)+4X(−11)=288−246−44=−2
これでやっと、余因子行列 adj A と行列式 |A| が求まりました。
そこで最後の計算を行ないます。

は下のように計算されます。
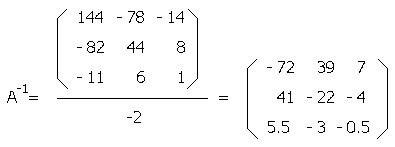
行列にある値を掛ける(または割る)計算は、行列の各要素にそれぞれその値を掛ける(割る)計算を行ないます。
ですから逆行列A−1は上の式の右辺になります。
やっと逆行列が求まりましたが、本日は時間がなくなってしまいました。
この続きは次回にいたします。
[2014.11.9追記]
今朝になりましてから読み直したところ、最後の逆行列A−1を求めるところの説明に一部間違っているところがみつかりましたので、訂正いたしました。
今は修正後の文になっています。
MYCPU80でCP/Mを![第64回]
2014.11.8upload
2014.11.9追記
前へ
次へ
ホームページトップへ戻る