超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第92回]
●倍精度関数について
明けましておめでとうございます。
本年もよろしくお願いいたします。
MYCPU80用のZB3DOS(CP/M互換DOS)もほぼ出来上がりました。
これからCP/M機能の動作確認の作業を行なう予定です。
それが済めばいよいよ供給開始となります。
いよいよ大詰めです。
さっそく年初からその作業に…。
というところなのですが、その前にやっておきたいことがありました。
それは倍精度関数(初等関数)のことです。
単精度の初等関数については長年の疑問が昨年やっと氷解し、その解法が「最良近似式」によるものであることがわかりました。
ZB3BASICには単精度の関数のほかに、倍精度の関数も搭載しております。
そちらのほうは単精度のような近似式が不明でしたために、テイラーの式をそのまま使っております。
せっかく最良近似式について理解を深めたことでもありますので、倍精度のほうもなんとかしたい、なんとかならないものか、という思いがありました。
CP/Mの検証作業にとりかかる前に、年明けのウォーミングアップも兼ねまして、まずはそのことについて、さぐってみることにいたしました。
単精度の関数についての最良近似式の計算はEXCELを使いました。
倍精度についても同じ手法が使えるとよろしいのですけれど…。
そこでちょいと気になりましたのが、EXCELの計算精度です。
一体EXCELはどの程度の精度で計算をしているのでしょうか?
そのあたりについて確認をしてみました。
下の表はEXCELでsinXを計算して、それとティラーの式での計算結果とを比較したものです。
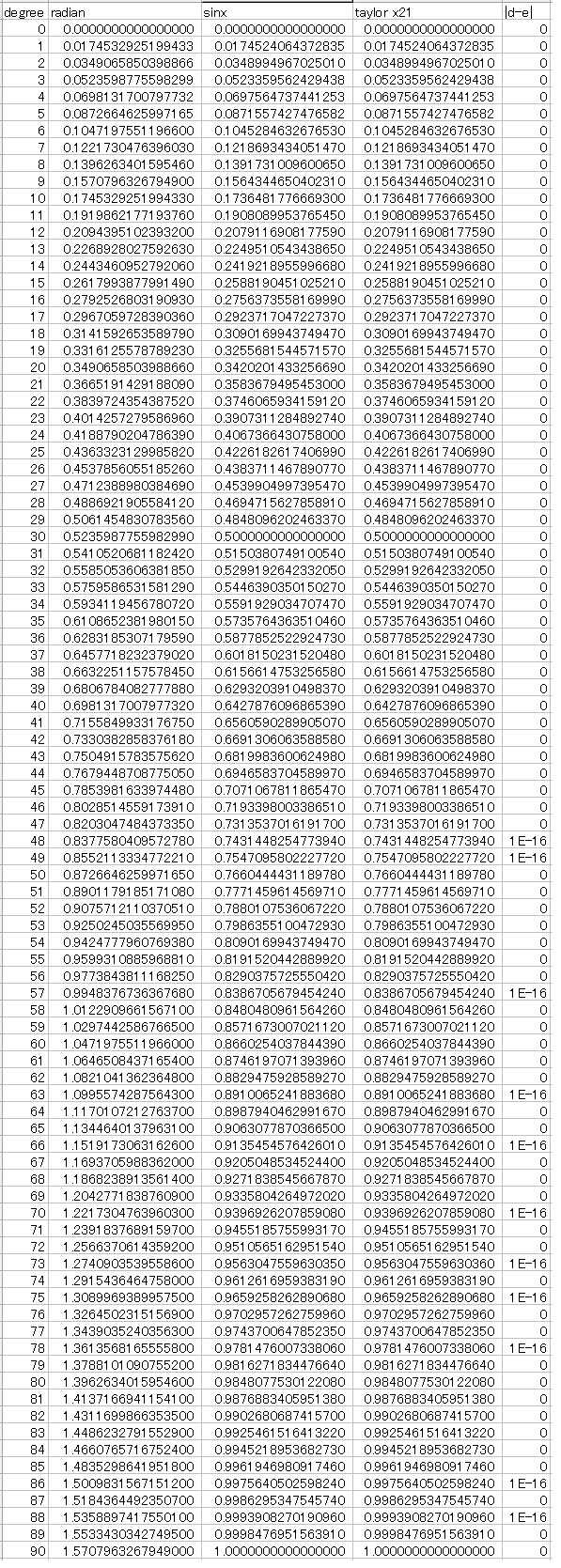
この表で見ますとEXCELは有効数字15桁の精度で計算をしているようです。
一方ZB3BASICの倍精度演算も同じ15桁です。
sin関数ではその精度を出すために、X21までの項を計算しています(下式)。
sinX=1−X3/3!+X5/5!−X7/7!+X9/9!−X11/11!+X13/13!−X15/15!
+X17/17!−X19/19!+X21/21!
テイラーの式もなかなかどうして立派なもので、X21までの項を計算すると、上の表のように有効数字15桁での誤差はほとんど0になります。
1E−16という誤差が出ているところがありますが、1x10−16ということですから許容の範囲内でしょう。
差を求めるとそういう結果になりますが、表示されている値には差はありません。
最下位を丸めて表示しているためだと思われます。
こういう結果から見て、sin関数については計算時間がかかることを別にすれば精度そのものは問題ないと考えてもよろしいでしょう。
それではもっと次数を少なくしたらどうなるでしょうか?
それも計算してみました。
下の表は上の表と同様にEXCELでsinXを計算して、それとティラーの式(X19の項までとX17の項まで)の計算結果とを比較したものです。
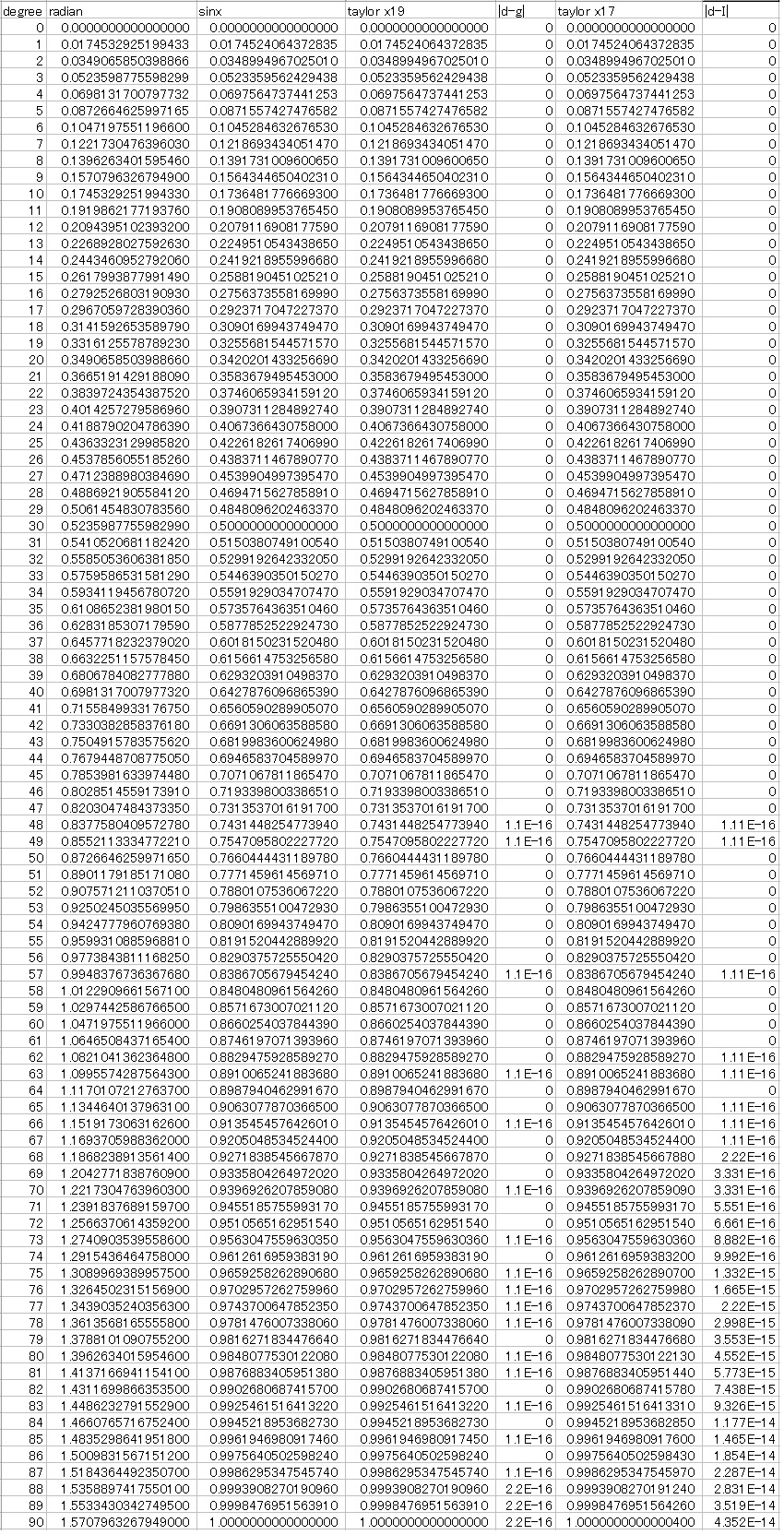
X17の項までの式ではさすがに誤差が目立つようになります。
たとえば X17の項までの最良近似式が求められれば、ひょっとすれば誤差を小さくすることができるかもしれません。
ですけれど…。
それがうまくできたとしてもたった2つの項を減らすことができるだけですから、ちょっと努力のしがいがないような気がします。
それにそもそも15桁の精度を求めるための計算を15桁の精度しかないEXCELを使って計算して本当に求めることができますでしょうか?
そこのところがちょいと疑問ではあります。
MYCPU80でCP/Mを![第92回]
2015.1.3upload
前へ
次へ
ホームページトップへ戻る