超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第93回]
●倍精度関数について(2)
年明け早々から記事の訂正です。
前回はEXCELの計算精度は有効数字16桁らしいと書きましたが、数値の桁を読み間違えておりました。
EXCELは有効数字15桁のようです。
おまけにEXCELの計算精度につきましてはすでに[第61回]で前回とほぼ同じ内容のことを書いておりました。
まことにお恥ずかしいことで、ほんとうに歳は取りたくないものであります。
さらにさらに、前回の記事は不正確なところがみつかりました。
前回の最後のところで、「15桁の精度を求めるための計算を15桁の精度しかないEXCELを使って計算して本当に求めることができますでしょうか」と書きましたが、その疑問は的中しておりました。
数学が得意な方でしたら考えるまでもないことだったかもしれませんが、私にはそのあたりのところが直感的にはどうも怪しいぞという気がしてはいても、理屈でこうこうだからと説明できなかったものですから、本日になりましてから、とにかくものはためしということで、さらに進んで検証をしていく中でたまたま前回の内容が不正確であったことがわかりました。
それがその計算精度に関係しておりました。
前回はsinXをテイラーの式でX21の項まで求めたところ、誤差が部分的に1×10−16のところがあって、X19の項までと、X17の項までの式ではその誤差が大きくなることについて、EXCELの計算結果を図示しながら説明しました。
次数を減らせば誤差が増えるというところはその通りだったのですが、誤差の大きさに誤りがありました。
実は前回のEXCELの表では誤差を絶対値で示しました。
その絶対値を計算するのに関数ABS()を使ったのでしたが、そこに新たな誤差が発生しておりました。
有効数字の限界のところで関数などを使えばどういうことになるかということを身をもって証明してしまったようなものです。
ABS()を外して絶対値ではなくて正負の値のままを表示させてみましたところ、下のようになりました。
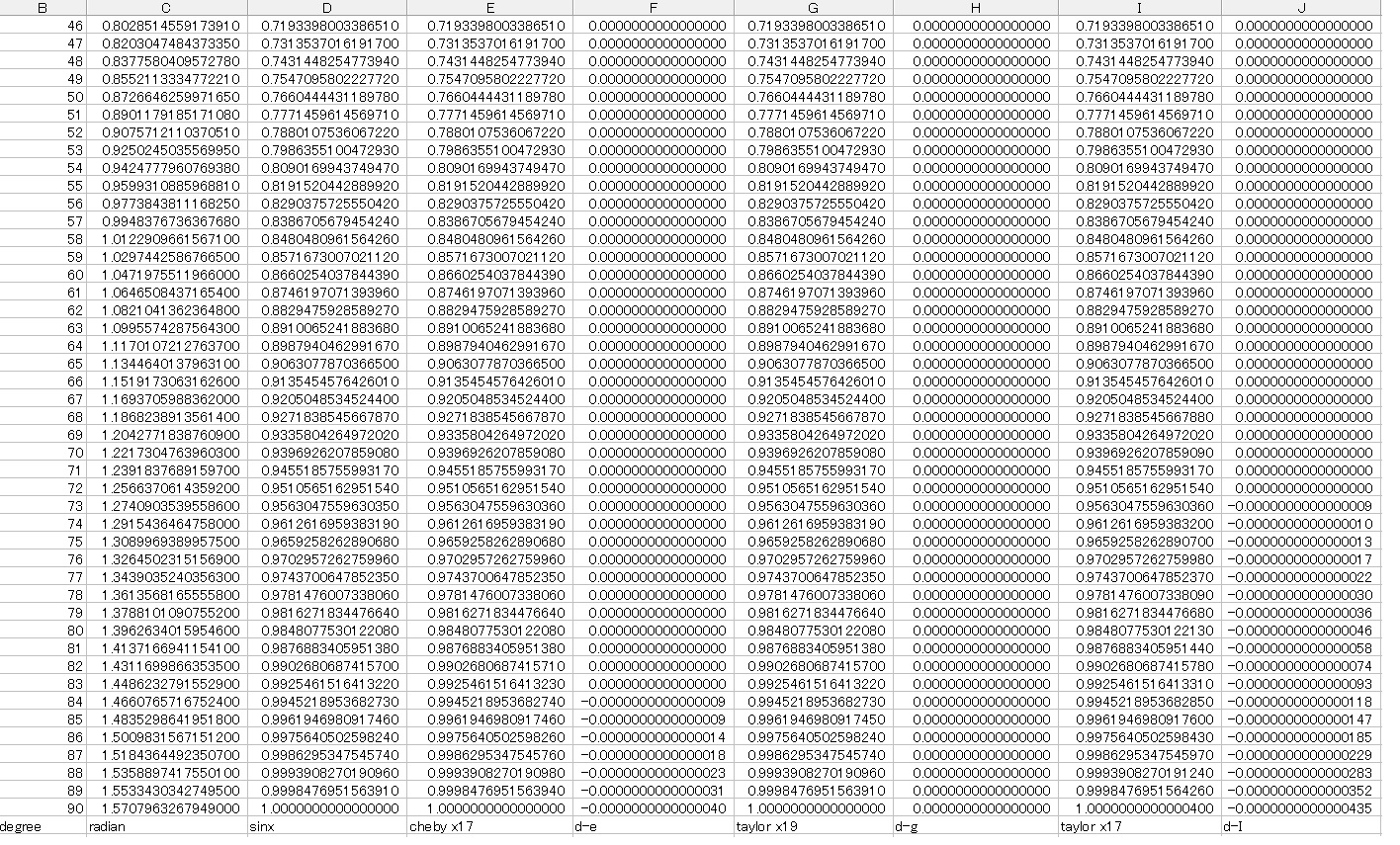
X21の項までの式について再確認するまでもなく、なんとX19の項までの式(G)でも誤差(H)は0になってしまいました。
前回のこの部分での誤差の犯人はABS()でした。
やっぱり計算精度の限界に近いところで誤差を正確に求めようとすることには無理があるようです。
ところで上の表ではcheby x17という列(E)があります。
そうなのです。
最良近似式を求める過程の式として、チェビシェフの近似式をX17の項まで求めてみたのです。
EXCELのsinXとの差は(F)列に出ています。
ずっと0できていますが84°〜90°のところでマイナスの誤差が出ています。
このチェビシェフの17次までの近似式のEXCELで計算したsinXに対する誤差とテイラーの17次までの式の同じくEXCELで計算したsinXに対する誤差のグラフは下のようになりました。
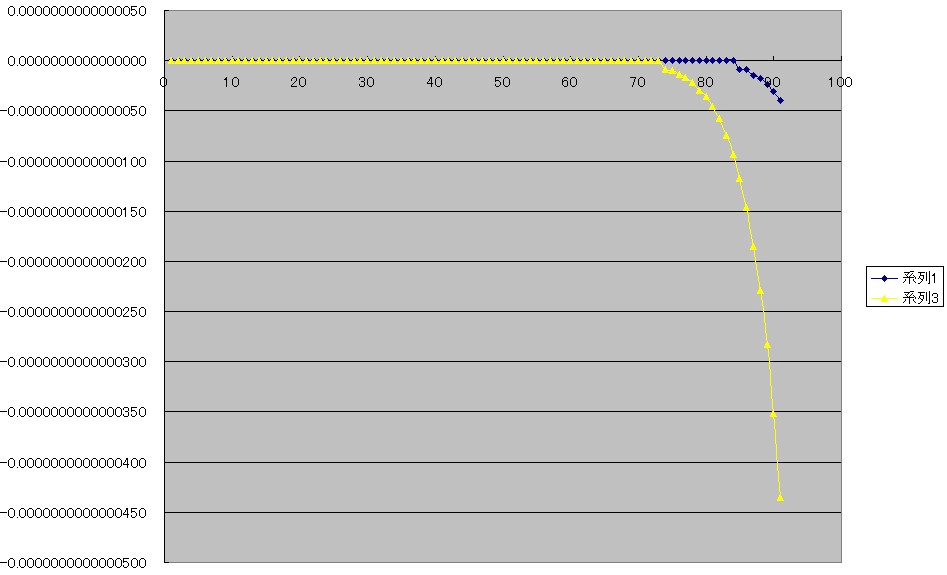
上のEXCELの表と、このグラフを見て、やっと気が付きました。
やっぱり計算精度15桁のEXCELで、同じ15桁の精度の最良近似式を求めることは、どだい無理な話でありました。
本日は時間がなくなってしまいました。
そのあたりのことにつきましては次回に書くことにいたします。
MYCPU80でCP/Mを![第93回]
2015.1.4upload
前へ
次へ
ホームページトップへ戻る