(ホントは74HC、CMOSなんだけど…)
[第148回]
●INR命令とJNZ命令を使ったプログラム
INR命令とJNZ命令を使ってテストプログラムを作りました。
0000 0C INR C
0001 C20000 JNZ 0000
0004 04 INR B
0005 C20000 JNZ 0000
0008 1C INR E
0009 C20000 JNZ 0000
000C 14 INR D
000D C20000 JNZ 0000
0010 2C INR L
0011 C20000 JNZ 0000
0014 24 INR H
0015 C20000 JNZ 0000
0018 3C INR A
0019 C30000 JMP 0000
本当は最初に全部のレジスタをゼロクリアしてからスタートすればよかったのですが、うっかりしていて、いきなりINR命令を書いてしまいました。
ですからプログラムをスタートしたとき、各レジスタの値が何であるのかわかりません(でも電源ON直後はたいていはFFになっています)。
プログラムの説明です。
まず最初にCレジスタを+1します。
結果が00でなければ、また0000番地に戻って、Cレジスタを+1します。
Cレジスタを+1した結果が00になったときだけ、次のアドレス0004にあるINR Bが実行されます。
Bレジスタを+1した結果が00でなければ、また0000番地に戻ってINR Cを実行します。
このプログラムはCレジスタが一番下位の8ビットで、それから上位にB、E、D、L、H、Aの順に8ビットのレジスタをつないだ、バイナリカウンタとして動作します。
CレジスタからAレジスタまで全部を順にカウントアップしていくようにプログラムを書いたのですが、念のため実行時間を計算してみたところ、上位にあるAレジスタとかHレジスタまではとても順番が回ってきそうにないことがわかりました。
実行時間を計算してみましょう。
●INR命令の実行時間
まずはINR命令の実行時間です。
INR命令のタイミングチャートは[第59回]にありますが、かなり時間が経ってしまいましたから、再掲することにいたします。
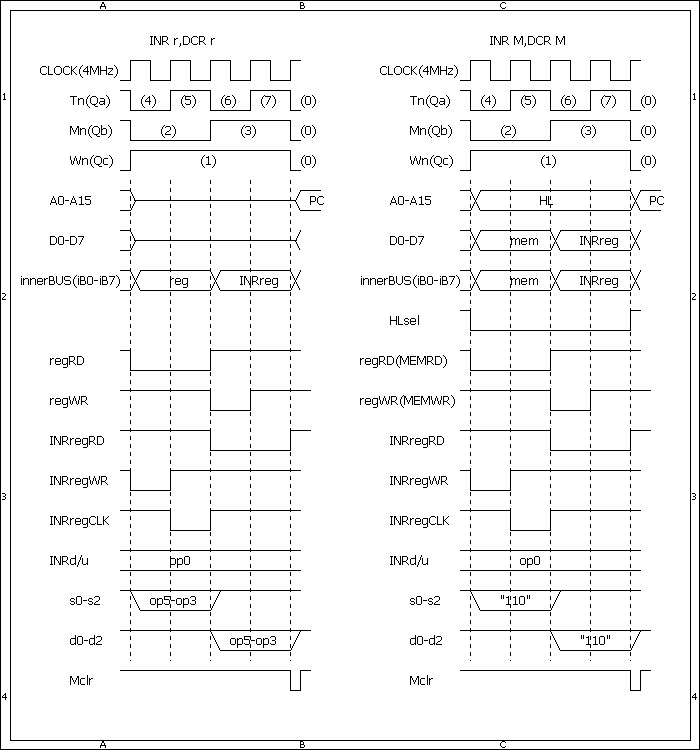
CLOCKは4MHzと書いてありますが、今回の試作から半分の2MHzに落としました。
Tnというのがマシンクロックになります。
T0〜T3は全命令共通でOPコードフェッチサイクル(メモリから命令コードを読んで、命令を解読するためのサイクル)です。
INR/DCR命令の所要クロックはそのT0〜T3を含めて、T0〜T7の8マシンクロックになります。
参考までに、8080のINR rは、5クロックです(8080はクロックといわずにステート(states)という語を使っていますが、当ホームページでは、クロックと言い換えて説明をすることにします)。
8080よりクロック数が多くなってしまうのは、一度データをINR/DCRレジスタに送り、そこでup/downカウントしてから、またもとのレジスタに戻すようにした仕組みのためです。
ちなみに、メモリに対する、INR M(DCR M)のクロック数も「つくるCPU」ではレジスタに対するのと同じ8クロックですが、8080では10クロックとなっています。
ということで、「つくるCPU」での、INR命令のクロック数は8クロックですから、INR命令を一回実行するのに必要な時間は、
0.5×8=4μsです(CPUクロックは2MHzですから、1クロックは0.5μsです)。
●JNZ命令の実行時間
次ははJNZ命令の実行時間です。
JNZ命令(JNZ以外の条件JMP命令も同じ)のタイミングチャートは条件が成立するときと成立しないときで異なってきます。条件が成立するときのタイミングチャートは普通のJMP命令と同じで、[第61回]で説明をしました。
条件が成立しないときのタイミングチャートは[第63回]で説明をしました。
しかし、いずれもかなり時間が経ってしまいましたから、再掲することにいたします。
JMP命令(および条件が成立したときのJX、JNX命令)のタイミングチャートです。
このタイミングチャートもCLOCK=4MHzとなっていますが、2MHzと読み替えてください(以後のチャートも同様です)。
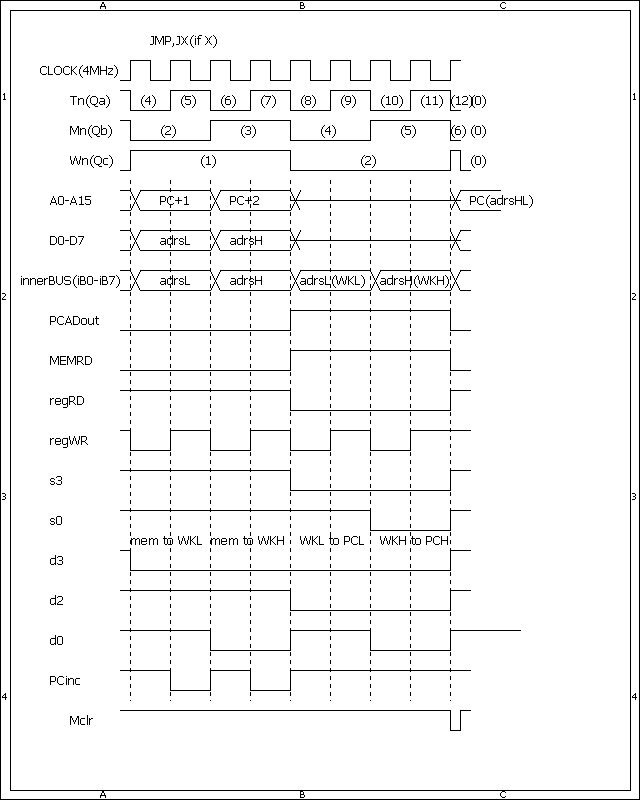
所要クロック数はT0〜T11の12クロックです。
実行時間は、
0.5×12=6μsです。
条件が不成立のときのJX、JNX命令のタイミングチャートです。
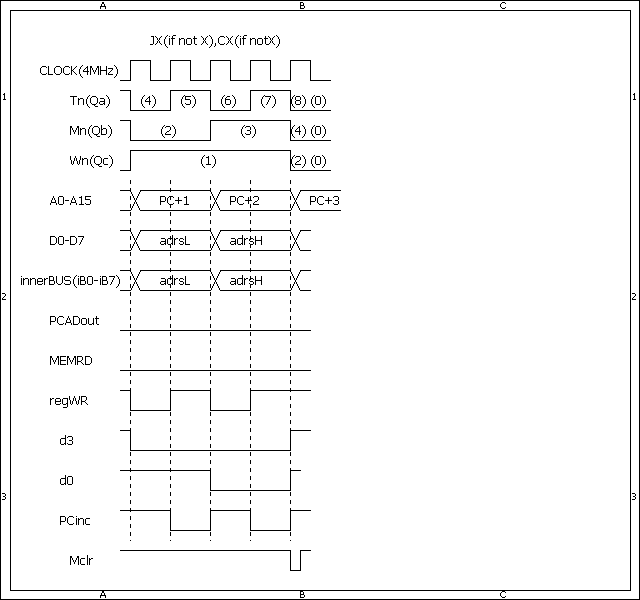
クロック数はT0〜T7の8クロックです。
実行時間は、
0.5×8=4μsです。
ちなみに8080の場合、JMP命令もJX、JNX(条件の成立、不成立にかかわらず)も、ともに10クロックです。
●プログラムの実行時間
さて、最初のテストプログラムに戻って、実行時間を計算してみます。
まず最下位のCレジスタが+1ずつカウントUPしながら、00〜FFまで一巡するには、INR命令とJNZ命令を256回実行します。
JNZ命令は256回のうち255回は≠0なので、条件が成立しますから1回につき6μs、1回のみは=0なので、条件が不成立ですから4μsです。
INRは256回、各4μsです。
したがってCレジスタが00〜FFまで一巡するには、
(4+6)×255+(4+4)=2558μsかかります。
Cレジスタが00になるごとに、その上位のBレジスタに対してINR命令とJNZ命令がそれぞれ1回ずつ実行されます。
そこで上のCレジスタでの計算結果を、Bレジスタが+1カウントUPするのに必要な時間、と言いかえることにすると、その実行時間は、
2558+(4+6)=2568μsということになります。
Bレジスタについても、Cレジスタの場合と同じで、2568μsかかるのが255回で、残り1回はそれより2μs短い2566μsになります。つまりBレジスタが00〜FFまで一巡するのに必要な実行時間は、
2568×255+2566=657406μsになります。
なおこの計算は別の方法で計算することもできます。
Bレジスタが00〜FFまで一巡する間にCレジスタに対するINRとJNZペアは256×256回実行され、Bレジスタに対するINRとJNZペアは256回実行されます。
そこで、Cレジスタ分として2558×256+Bレジスタ分2558を計算すると、
654848+2558=657406μsになります。
うーん。こちらの方がわかりやすそうですね。
657.4msですから、Bレジスタの最上位ビットが点滅するのは、なんとか確認できそうです。
そのさらに上位のEレジスタが00〜FFまで一巡するのに必要な実行時間は、
Bレジスタでの後の計算方法に従うと、
Bレジスタ分として657406×256+Eレジスタ分2558=168295936+2558=168298494
になります。
168.3秒です。
すると、その上位のDレジスタが一巡するには、168.3×256=43084.8秒もかかってしまいます。
43084/60≒718分ですから、718/60≒12時間(!)かかります。
これじゃあ、そのさらに上位のLレジスタが一巡するまでは、とてもつきあえません。
つきあえませんけれど、参考までに考えてみてください。
最上位のAレジスタが一巡するのに必要な時間はどれくらいだと思います?
Dレジスタが一巡するのに12時間かかります。
するとその上位のLレジスタが一巡するには、
12時間=0.5日ですから、
0.5×256=128日かかりますねえ。
ここまでは、まだなんとかかろうじて、常識の範囲です。
でも、その上のHレジスタとなると、
128×256=32768日≒90年(!)
いきなり、非常識の世界に突入してしまいます。
Hレジスタが一巡するまでに、私は勿論のこと、読者の皆様も、多分ほとんどのお方が、残念ながら、灰になってしまいますねえ。
とすると、最後のAレジスタが一巡するには…。
うーん…。計算しても、もはや無意味ですから、止めておきましょう。
ですから、今回のテストプログラムの、INR HとINR Aは、どうせ実行できませんから、無駄な命令ということになります。
時として、勢いでこういう無意味なプログラムを書いてしまうことがある、という悪い見本です。
あ。
INR Lまでは意味がありますから、全部が悪いわけではありませんですよ。
次回は、このプログラムを実行しているところの写真をお見せします。
2009.1.27upload
前へ
次へ
ホームページトップへ戻る